Centro di massa e moto del centro di massa (parte prima)
Febbraio 19th, 2021 | by Marcello Colozzo |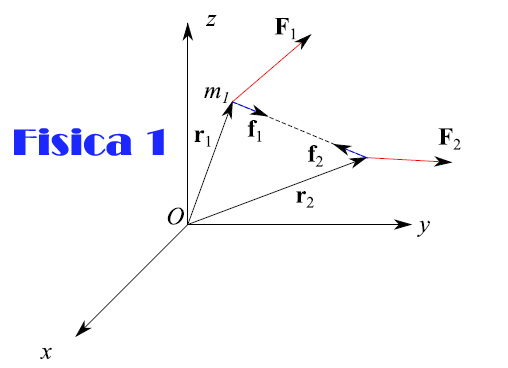
Nella lezione precedente abbiamo asserito che in molti casi un sistema meccanico può essere schematizzato da un unico punto in cui si suppone concentrata la massa del sistema medesimo. Per dimostrare in maniera rigorosa tale asserzione consideriamo dapprima il caso più semplice: un sistema meccanico costituito da due masse m1 e m2, ciascuna delle quali schematizzabile attraverso un punto materiale. Supponiamo poi che il sistema sia sottoposto a forze esterne. Precisamente una forza F1 agente su m1 e una forza F2 agente su m2. L'interazione reciproca è invece rappresentata da due forze f e -f, che rappresentano manifestamente le forze interne. Applichiamo poi il secondo principio della dinamica alle singole masse, ottenendo due equazioni differenziali vettoriali, ciascuna per ogni particella. A questo punto è facile definire la massa totale e un vettore posizione rc dato dalla media ponderata dei vettori posizione di singola particella, per poi verificare che il corrispondente punto posizionato in rc si muove come un punto materiale soggetto alla sola risultante delle forze esterne, e avente massa pari alla massa totale del sistema. Ed è appunto questa la definizione di centro di massa di un sistema meccanico. Risultato facilmente generalizzabile a un sistema di n particelle.
In the previous lesson we have asserted that in many cases a mechanical system can be schematized from a single point where the mass of the system is supposed to be concentrated. To rigorously demonstrate this assertion, we first consider the simplest case: a mechanical system consisting of two masses m1 and m2, each of which can be schematized through a material point. Then suppose that the system is subjected to external forces. Precisely a force F1 acting on m1 and a force F2 acting on m2. The reciprocal interaction is instead represented by two forces f and -f, which manifestly represent the internal forces. We then apply the second principle of dynamics to the individual masses, obtaining two vector differential equations, each for each particle. At this point it is easy to define the total mass and a position vector r
Tags: centro di massa, moto del centro di massa, sistemi di punti materiali
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











