» Esercizi svolti di Matematica e Fisica

[¯|¯] Introduzione al formalismo matematico della Meccanica quantistica. L'equazione di Schrödinger

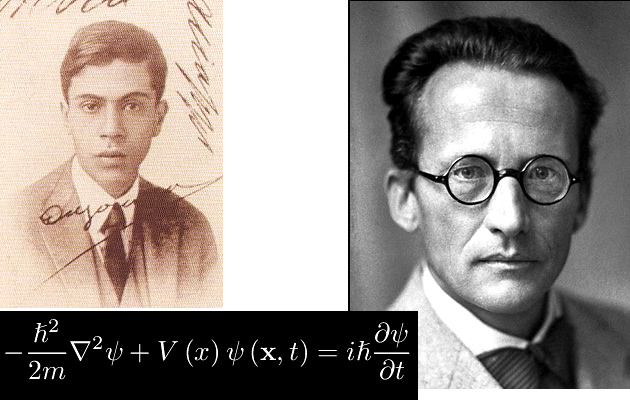
Il formalismo matematico della Meccanica quantistica è estremamente complicato, in quanto richiede nozioni di analisi funzionale. Non a caso, Ettore Majorana scriveva nel 1938 nei suoi Appunti per la prolusione ai corsi:

Per esporre la meccanica quantistica nel suo stato attuale esistono due metodi pressoché opposti. L'uno è il cosiddetto metodo storico: ed esso spiega in qual modo, per indicazioni precise e quasi immediate dell'esperienza, sia sorta la prima idea del nuovo formalismo; e come questo si sia successivamente sviluppato in una maniera obbligata assai più dalla necessità interna che non del tenere conto di nuovi decisivi fatti sperimentali. L'altro metodo è quello matematico, secondo il quale il formalismo quantistico viene presentato fin dall'inizio nella sua più generale e perciò più chiara impostazione, e solo successivamente, se usato in maniera esclusiva, presenta inconvenienti molto gravi.
È un fatto che, quando sorse la meccanica quantistica, essa incontrò per qualche tempo presso molti fisici sorpresa, scetticismo e perfino incomprensione assoluta, e ciò soprattutto perché la sua consistenza logica, coerenza e sufficienza appariva, più che dubbia, inafferrabile. Ciò venne anche, benché del tutto erroneamente, attribuito a una particolare oscurità di esposizione dei primi creatori della nuova meccanica; ma la verità è che essi erano dei fisici, e non dei matematici, e che per essi l'evidenza e giustificazione della teoria consisteva soprattutto nell'immediata applicabilità ai fatti sperimentali che l'avevano suggerita.
[...]
Questi strumenti matematici in gran parte preesistevano al sorgere della nuova meccanica (come opera disinteressata di matematici che non prevedevano un così eccezionale campo di applicazione), ma la meccanica quantistica li ha «sforzati» e ampliati per soddisfare alle necessità pratiche.

In questo handbook ricaviamo l'equazione di Schrödinger per un sistema quanto-meccanico costituito da una particella di massa m che compie un moto unidimensionale. Il formalismo viene ricavato in maniera "quasi" intuitiva utilizzando nozioni di Analisi matematica, mostrando al contempo l'analisi funzionale quale evoluzione della prima nel senso che al posto del consueto spazio euclideo R^n considera "spazi funzionali" ovvero spazi in cui i "punti" sono funzioni. Di seguito gli argomenti:

La nozione di spazio funzionale

• Introduzione
• Moto di un punto nello spazio ordinario
• Lo spazio funzionale C([a,b])
• Endomorfismi in C^p([a,b])
• Autofunzioni e autovalori
• Polinomi di Legendre
• Polinomi di Hermite

Il formalismo matematico della meccanica quantistica

• "Moto" di un "punto" in uno spazio ordinario
• Traslazione spaziale ed evoluzione temporale
• Le osservabili posizione e impulso. L'equazione di Schrödinger

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: equazione di schrödinger, meccanica quantistica