» Esercizi svolti di Matematica e Fisica

Esperimenti computazionali con Mathematica: la trasformata di Fourier di f(t)=t+2pi*sin(w0*t)

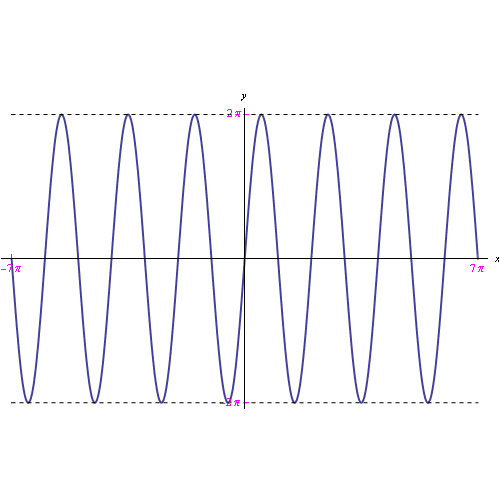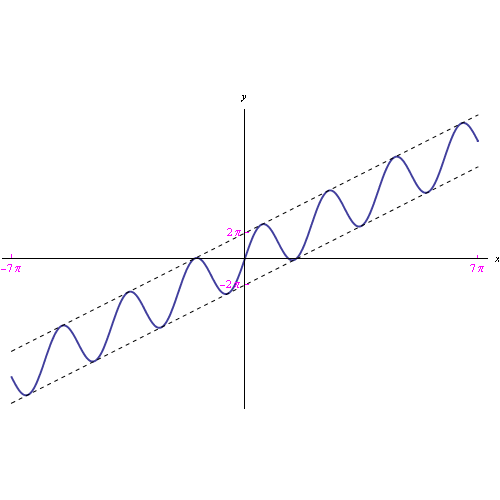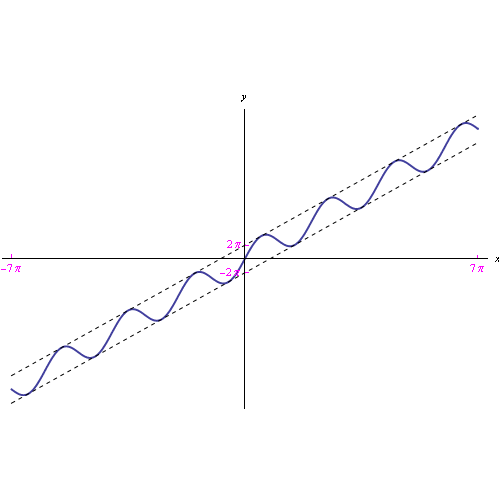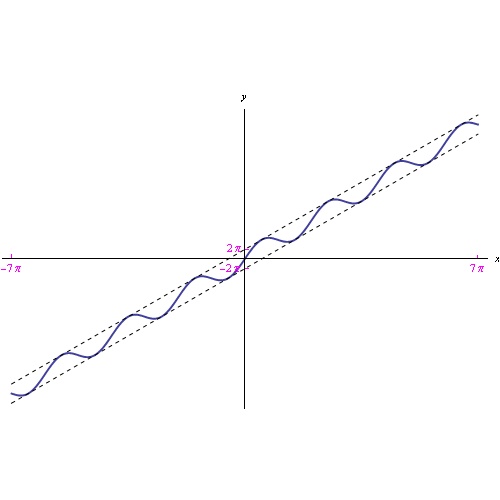
Rilasciata la prima versione dell'handbook Esperimenti computazionali con Mathematica: la trasformata di Fourier di f(t)=t+2*pi*sin(w0*t).

Argomenti:

1. Comportamento all'infinito della funzione f(x)=x+2pi*sin(x)
   In questa sezione mostriamo che la funzione f(x) pur contenente il termine periodico sin(x) è regolare all'infinito (nel senso che è ivi dotata di limite). Più precisamente, diverge positivamente per x->+oo e negativamente per x->-oo












2. La trasformata di Fourier di f(t)=t+2pi*sin(w0*t)

Qui abbiamo la stessa funzione nel dominio del tempo. Come è noto, per una funzione del tipo sin(w0*t) la trasformata di Fourier non esiste come funzione, ma come distribuzione. Nel caso in esame, la situazione è diversa poichè abbiamo una funzione non periodica. Esaminiamo comunque un algoritmo che ci permette di avere un'idea dell'andamento della TF.

Scarica l'handbook

Tags: delta di dirac, Trasformata di Fourier