» Esercizi svolti di Matematica e Fisica

[¯|¯] L'equazione di conduzione del calore. Caso unidimensionale. Il metodo di Fourier

Ottobre 11th, 2018 | by Marcello Colozzo |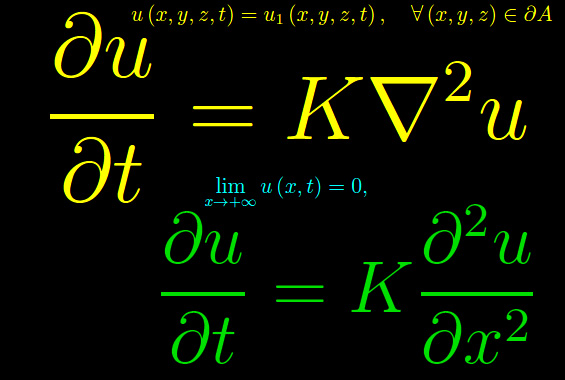

Premessa

L'ottimizzazione termica di una cantina è un difficile problema di Fisica Matematica, le cui origini si perdono nella notte dei tempi. Incidentalmente, per cantina termica ideale si intende una classe di soluzioni dell'equazione differenziale alle derivate parziali che regola la conduzione del calore dalla superficie terrestre verso una quota assegnata nella verticale passante per un punto della superficie della Terra, ed orientata verso il centro del pianeta (in approssimazione sferica).

Per la ricerca delle soluzioni, si assume che la temperatura in superficie sia una assegnata funzione periodica di periodo T (pari a un anno) che denotiamo con u₀(t). Supponendo che siano verificate le condizioni di Dirichlet, si sviluppa in serie di Fourier tale funzione, per poi imporre che la soluzione dell'equazione alle derivate parziali, sia a sua volta sviluppabile in serie di Fourier, ma con coefficiente che ovviamente dipendono dalla variabile spaziale x (profondità). In tal modo, il calore che si propaga nella Terra è interpretabile attraverso un campo scalare u(x,t) noto come onda termica. A questo punto il gioco è fatto, perchè l'idealizzazione termica della cantina (fresca d'estate e calda di inverno) richiede la determinazione della quota x tale che a un massimo della temperatura in superificie corrisponda un minimo dell'onda termica calcolata in x.
In questo modo, ottimizzando termicamente la cantina, abbiamo ricondotto il difficile problema dell'integrazione di un'equazione differenziale alle derivate parziali all'integrazione di un'equazione differenziale ordinaria, che è molto più semplice.
Lo step successivo, consiste nell'assumere la presenza di fluttuazioni di temperatura in superficie, i.e. immergere la u0(t) in un white noise

Conduttore unidimensionale

Consideriamo il caso in cui il corpo C sia un conduttore termico lineare, cioè rappresentabile da un segmento di estremi P e Q. Orientando un asse x per i predetti punti nel verso per il quale P precede Q, si ha nelle notazioni del numero precedente

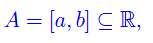
dove a,b sono le coordinate di P e Q rispettivamente, nel predetto riferimento cartesiano R(Ox). L'equazione di conduzione del calore assume la forma:

essendo u(x,t) il campo di temperatura lungo C. Se quest'ultimo non è infinitamente esteso, si ha a,b appartenti al campo reale R, onde

le cui condizioni al contorno sono:

dove u0(t) e u1(t) sono funzioni assegnate. Per una ragione che apparirà chiara nel prossimo post, è interessante il caso

corrispondente a un conduttore C infinitamente esteso. Dal momento che il campo di temperatura si annulla all'infinito nelle coordinate spaziali, le precedenti condizioni al contorno si riscrivono:

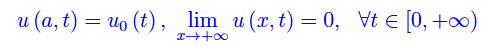
Se si è interessati alla sola soluzione di regime, non occorre fissare una condizione iniziale per la predetta equazione.

Il metodo di Fourier. Impostazioni

Esaminiamo il caso in cui u0(t) sia una funzione periodica di periodo T:

E se u0(t) verifica le condizioni di Dirichlet:

dove ω=2π/T, mentre i coefficienti di Fourier sono dati dalla nota relazione:

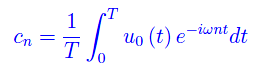
Imponiamo che

sia soluzione dell'equazione di conduzione, supponendo che la predetta serie sia derivabile termine a termine, onde

Segue

Cioè

ovvero la serie di Fourier della funzione

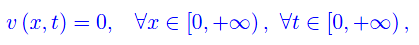
i cui coefficienti di Fourier sono tutti nulli:

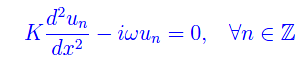
n altri termini, le infinite funzioni un(x) che compaiono nello sviluppo in serie risolvono la seguente equazione differenziale ordinaria

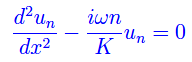
Tags: condizioni al contorno, equazione di conduzione del calore, equazioni differenziali alle derivate parziali, metodo di fourier

Articoli correlati