[¯|¯] Funzioni ricorsivamente convergenti
Febbraio 9th, 2017 | by Marcello Colozzo |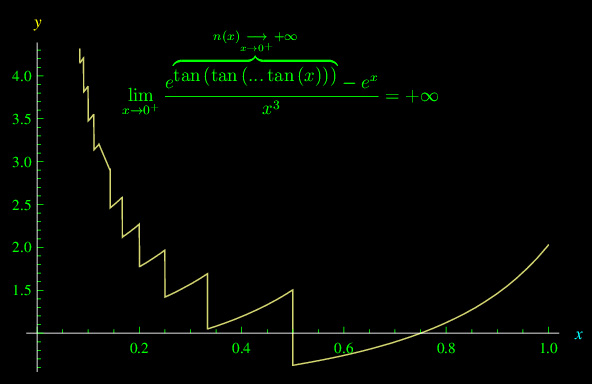
Fig. 1
L'esercizio precedente si presta ad una ulteriore generalizzazione, introducendo le nozioni di ricorsione e di convergenza ricorsiva. In realtà abbiamo già affrontato tale problema in .
Modifichiamo, aggiungendo ricorsività, il predetto esempio nel modo che segue
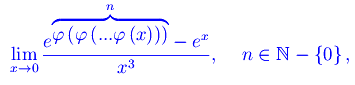
dove φ(x) è una funzione assegnata, infinitesima in x=0 e derivabile in un intorno di tale punto un numero "sufficiente" di volte in modo da poter applicare la regola di De L'Hospital in modo da risolvere la forma indeterminata 0/0. Esplicitando alcuni valori di n:
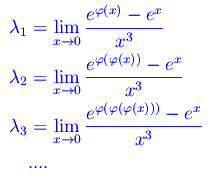
Definizione
La funzione
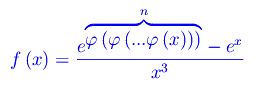
è, per x->0, ricorsivamente convergente se

Ciò equivale a dire che per x->0
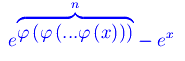
è un infinitesimo di ordine 3, per ogni intero naturale non nullo n.
Nel caso della funzione φ(x)=tan(x), proponiamo la dimostrazione di Davide Lombardi.
Tale tipo di convergenza può essere studiata attraverso l'ausilio di un software del tipo Mathematica. Ad esempio, possiamo porre
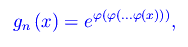
cosicché il limite si scrive
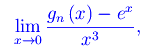
dopodiché si cerca di applicare la regola di De L'Hospital. Tuttavia, per come abbiamo definito la convergenza ricorsiva, il limite deve essere calcolato per ogni n, cosa ovviamente impossibile. Al più, si potrebbe ricorrere a un procedimento di tipo induttivo vincolato, ovviamente, alla funzione φ(x). Ad esempio, per φ(x)=tanx, Mathematica restituisce i seguenti risultati:
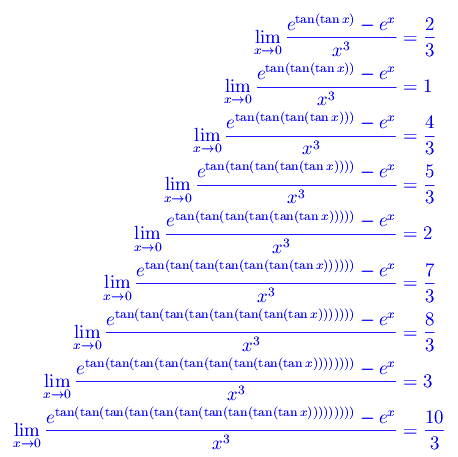
Sembra quindi che la funzione sia ricorsivamente convergente. Ciò potrebbe rappresentare un risultato generale. Cioè
Congettura
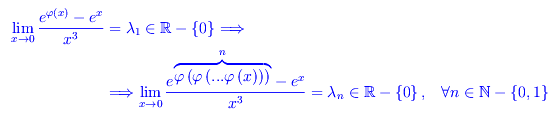
A questo punto ci sembra più interessante studiare la ricorsività locale per ciò che riguarda la convergenza della funzione
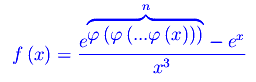
per ricorsività locale intendiamo la circostanza secondo cui per x->0 il numero di ricorsioni diviene infinitamente grande. Cioè
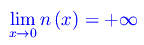
Formalmente f(x) diviene una funzione di due variabili:
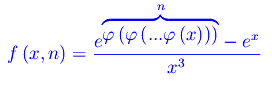
definita nel seguente sottoinsieme di R²:
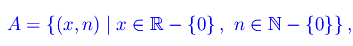
passando poi alla funzione composta della sola variabile x:
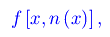
onde si tratta di studiare il limite
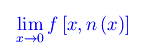
Dal momento che n è un intero naturale, siamo tentati di porre
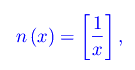
dove [.] denota la parte intera. Per φ(x)=tan x otteniamo - con l'ausilio di Mathematica - il grafico di fig. 1, dove per necessità computazionali abbiamo considerato il comportamento in un intorno destro di x=0. Da tale andamento sembra che la funzione sia ricorsivamente (in senso locale) divergente per x->0.
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.
Tags: Funzioni ricorsivamente convergenti, Funzioni ricorsivamente divergenti, limiti, ricorsività locale
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











