[¯|¯] La regola di De L'Hospital
Gennaio 26th, 2017 | by Marcello Colozzo |
La regola di De L'Hospital è l'applicazione di due teoremi che richiedono la conoscenza della nozione di derivata, per cui in questo post ci limitiamo semplicemente ad enunciarla.
Siano date le funzioni
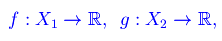
entrambe infinitesime o entrambe infinite in un punto
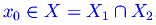
Quindi il rapporto f(x)/g(x) si presenta, per x->x0, in una delle forme indeterminate (0/0),(oo/oo). Se sono verificate le seguenti ipotesi:
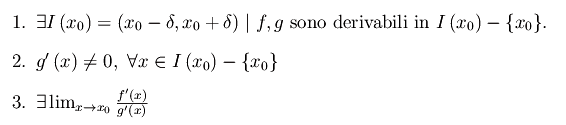
Allora
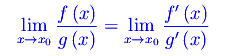
In generale, quando si applica la regola di De L'Hospital è consuetudine utilizzare la notazione simbolica:
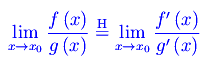
Esempio
Dimostrare
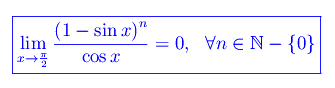
Svolgimento
Applicando la regola di De L'Hospital per n=1:
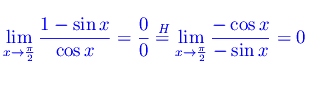
Per n>1:
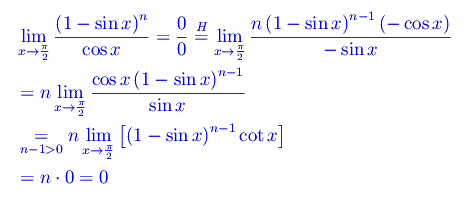
No TweetBacks yet. (Be the first to Tweet this post)
Tags: Forme indeterminate, limiti, regola di de l'hospital, teoremi di De L'Hospital
Articoli correlati
Congettura di Riemann
Trasformata discreta di Fourier
Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier 
Infinitesimi ed infiniti
Limiti notevoli
Punti di discontinuità
Misura di Peano Jordan
Eserciziario sugli integrali
Differenziabilità 
Differenziabilità (2)
Esercizi sui limiti
Appunti sulle derivate
Studio della funzione
Esercizi sugli integrali indefiniti
Algebra lineare
Analisi Matematica 2
Analisi funzionale
Entanglement quantistico
Spazio complesso
Biliardo di Novikov
Intro alla Meccanica quantistica
Entanglement Quantistico
