[¯|¯] La legge di distribuzione dei numeri primi
Aprile 16th, 2017 | by Marcello Colozzo |
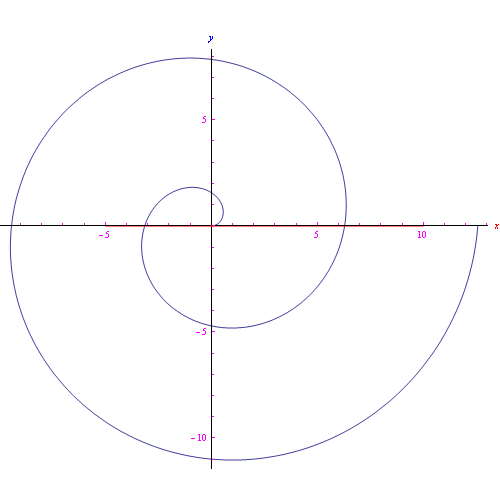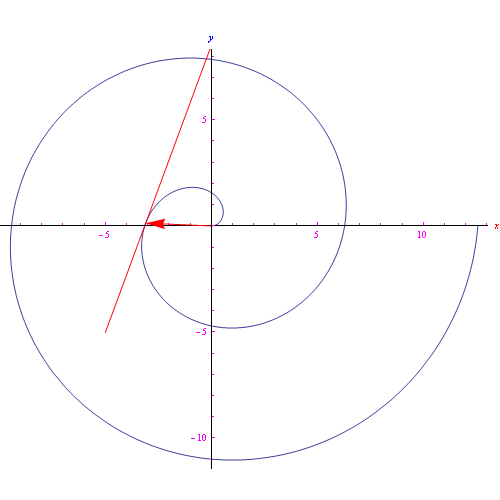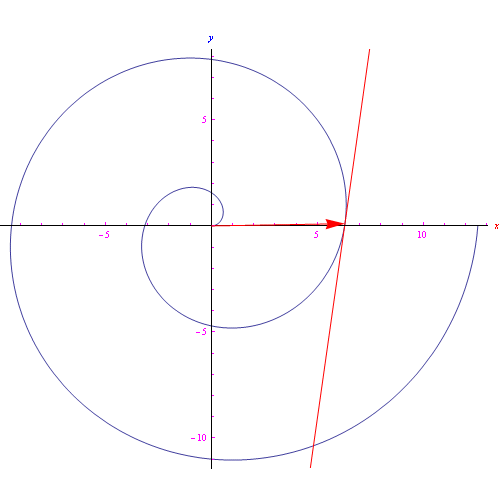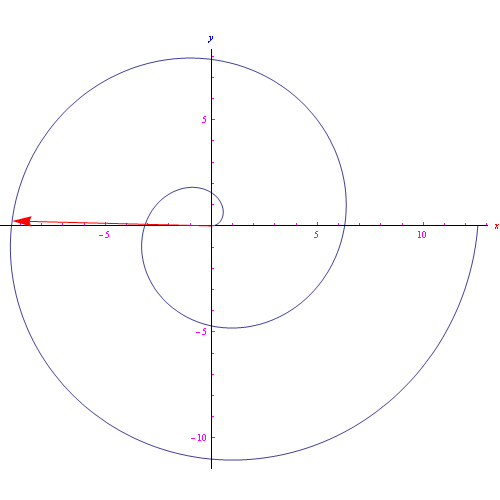
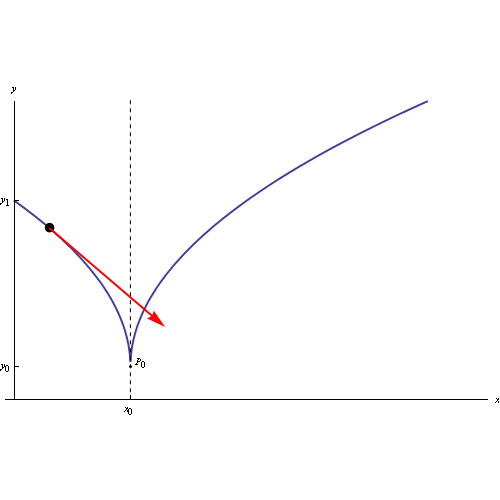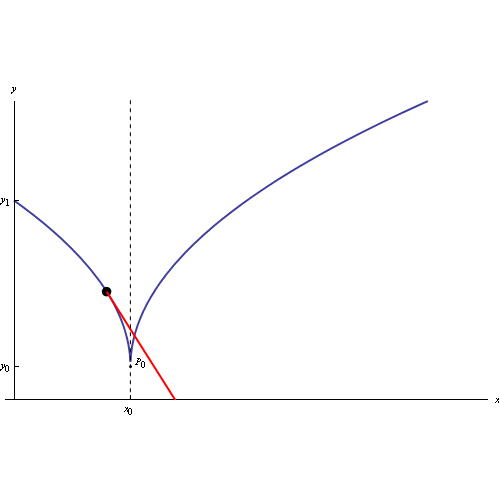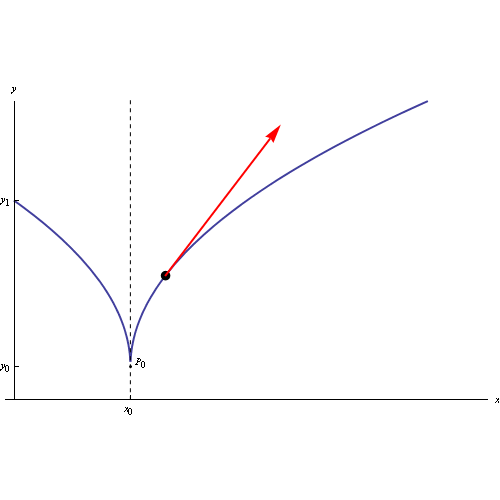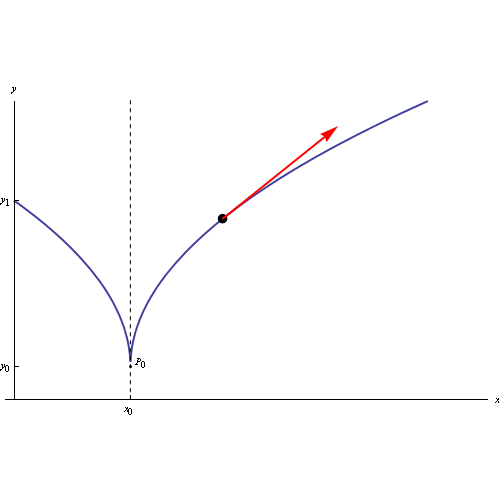
Fig. 1
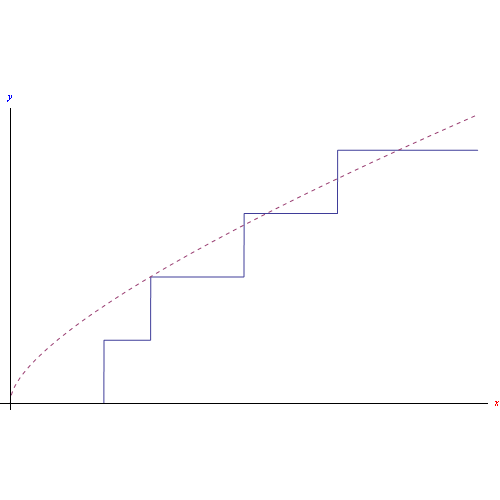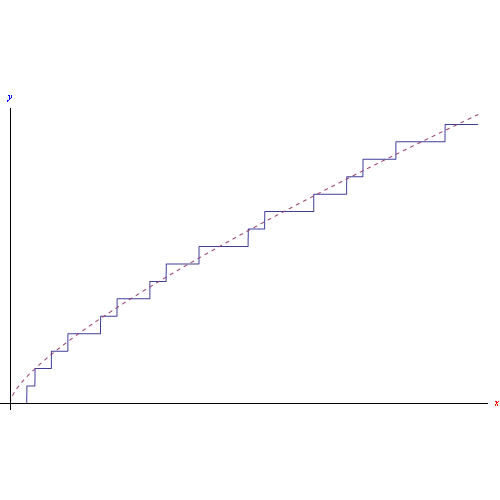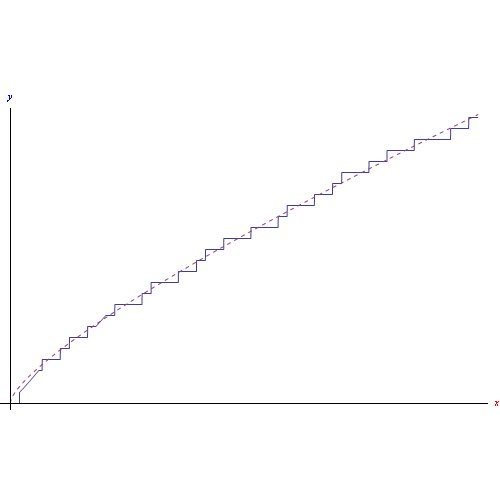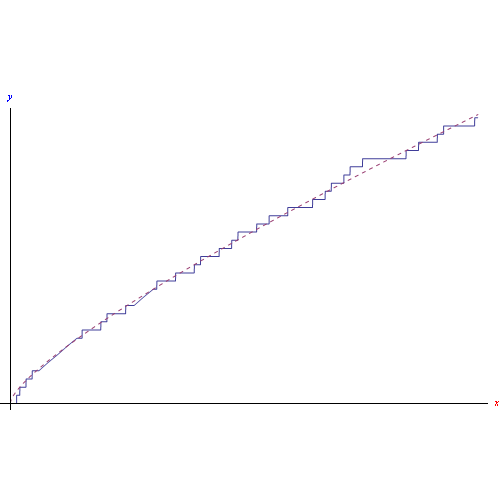
Fig. 1
La funzione a gradini π(x)
Come è noto, i numeri primi sono elementi di N che ammettono solo divisori banali. Cioè, p è numero primo se e solo se p è divisibile solo per se stesso e per 1. I numeri primi compongono una successione di elementi di N:
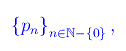
dove pn è l'n-esimo numero primo. Ad esempio, p1=2,p2=3,p3=5,p6=7,p7=11,... La successione così definita è un'applicazione iniettiva:
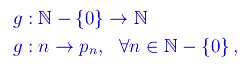
il cui grafico è
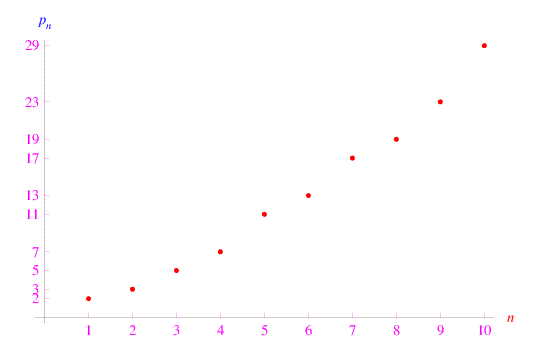
Dall'iniettività segue l'invertibilità di g:
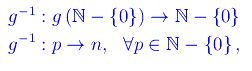
dove g(N-{0}) è l'immagine di N-{0} attraverso g. Ad esempio: g(3)=5=>g-1(5)=3. Pertanto per un assegnato numero primo p,g-1 è il numero di primi tra 1 e p, per cui la funzione g-1 definisce la legge di distribuzione dei numeri primi. È istintivo prolungare g-1 da g(N-{0}) a tutto N. Ridifinendo:
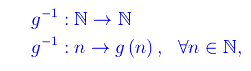
Il problema consiste nel trovare l'espressione analitica dell'applicazione g-1. Per poter attaccare tale problema con i metodi dell'Analisi matematica, è necessario prolungare tale applicazione da N a [0,+oo), onde definiamo:
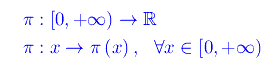
che è una funzione reale della variabile reale x tale che π(x) è il numero di primi tra 0 e [x], dove il simbolo [.] denota la parte intera di un numero reale. La funzione π(x) è non negativa ed è continua a tratti, giacchè ha una
discontinuità di prima specie in tutti e soli i punti le cui ascisse sono numeri primi. Invero, denotando con D l'insieme dei punti di discontinuità di π(x), si ha:
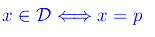
In figura. riportiamo il grafico della restrizione di π(x) all'intervallo X=[0,6]
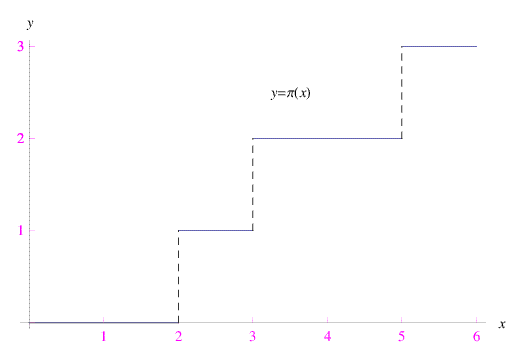
da cui vediamo che:
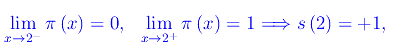
Per X=[0,20], otteniamo il grafico
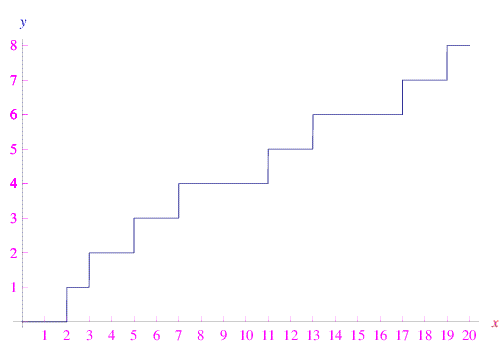
Per X=[0,200]
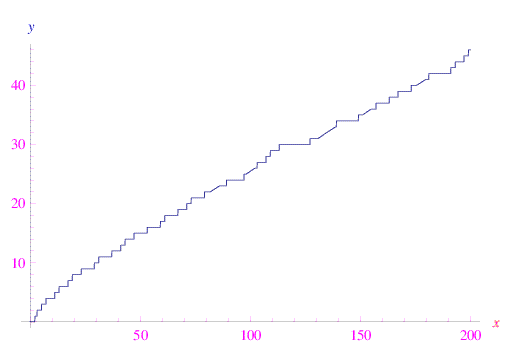
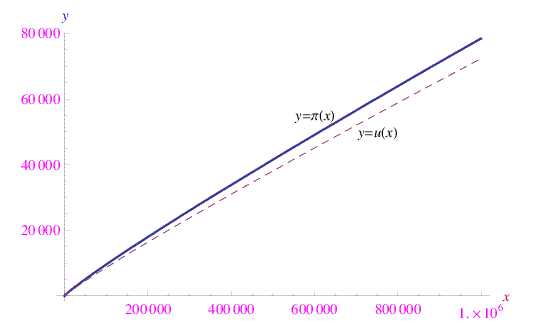
Al crescere indefinito di x, le discontinuità sono meno evidenti, per cui è possibile tentare un'approssimazione "globale" di π(x) con una funzione continua in [0,+oo). Tale approccio è giustificato dal grafico seguente, da cui notiamo la leggera curvatura del diagramma per x<200000, che esprime la non linearità della funzione. Si dimostra che nel limite dei grandi x, il grafico è concavo verso il basso. Ciò si traduce in una diminuzione della densità dei numeri primi.
Per ogni numero primo:
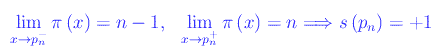
Il Teorema dei Numeri Primi. L'approssimazione di Riemann
Riguardo al comportamento asintotico di π(x), sussiste il seguente teorema:
Teorema
Per x->+oo, π(x) e u(x)=x/(ln x) sono infiniti equivalenti Cioè:
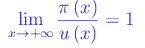
Per la dimostrazione rimandiamo a Analytic Number Theory.
La fig. seguente confronta il grafico di π(x) con quello di u(x).
In forza del comportamento "complicato" della funzione π(x), ci aspettiamo che quest'ultima non sia elementarmente esprimibile. Incidentalmente, una funzione che approssima π(x) fu scoperta da Riemann e si esprime attraverso la funzione logaritmo integrale:
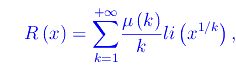
dove µ(k) è la funzione di Möbius:
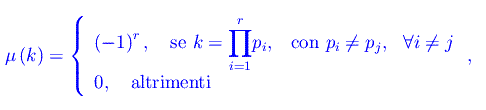
mentre li(x) è la funzione logaritmo integrale:
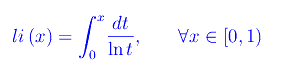
Osserviamo che la funzione integranda ha una discontinuità rimovibile in x=0, da cui la sua sommabilità in [0,1). Inoltre:
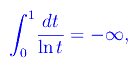
per cui:
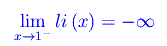
La R(x) è maledettamente complicata, in quanto nella sommatoria compaiono i seguenti termini:
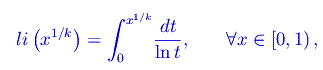
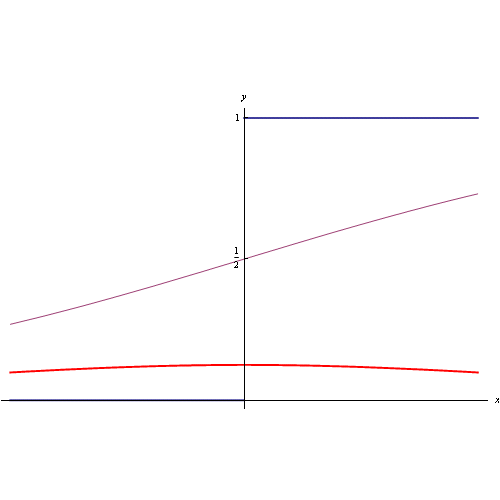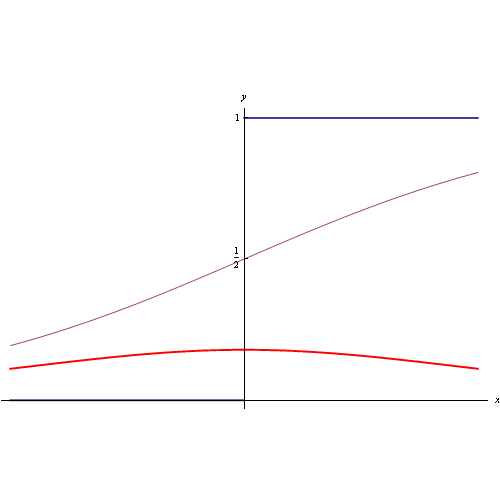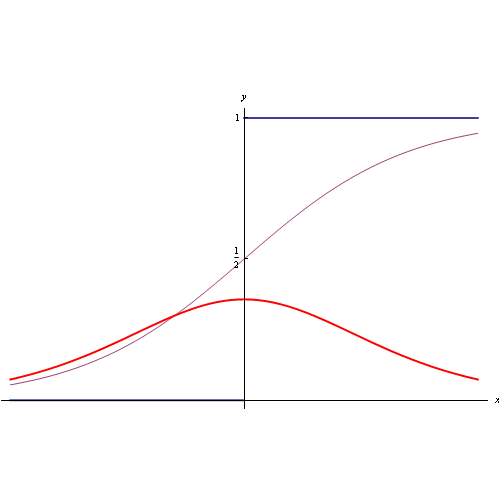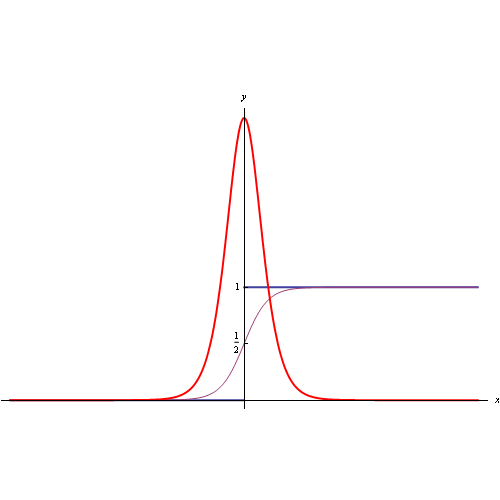
Nel suo libro Ilan Vardi fornisce il codice Mathematica per calcolare/plottare la funzione R(x) a partire da una espressione equivalente a quella precedente che si svincola dalla funzione di Möbius:
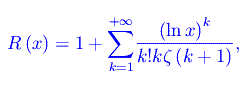
dove ζ è la zeta di Riemann. Per calcolare/plottare la funzione R(x), dobbiamo approssimare la serie alla sua somma parziale di ordine N:
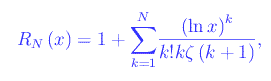
risultando:
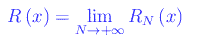
Per avere 15 cifre di precisione di x<10¹², è sufficiente porre N=100, ottenendo vari andamenti racchiusi nell'anmazione grafica di fig. 1.
Riassumendo: Siamo partiti dalla successione {pn} che può essere riprodotta (fino a un assegnato n»1) da un qualunque ambiente di calcolo numerico. Per poter affrontare il problema della determinazione della legge con cui si distribuiscono i termini pn della successione, abbiamo dapprima considerato l'inversa di tale funzione, per poi considerarne l'estensione al campo reale, ottenendo la funzione a gradini π(x). Grazie alla formula approssimata di Riemann, siamo giunti a una buona approssimazione non-locale di π(x). Notiamo incidentalmente due aspetti particolari della formula approssimata:
- R(x) non è elementarmente esprimibile, in quanto espressa attraverso la somma di una serie.
- .Nell'espressione equivalente di R(x) notiamo la presenza di uno strano oggetto", ovvero della funzione zeta di Riemann che svolge un ruolo cruciale nella legge di distribuzione dei numeri primi.
Le circostanze 1 e 2 suggeriscono che siamo ancora lontanissimi nel trovare una soluzione al problema proposto che - ricordiamolo - consiste nell'approssimare la funzione π(x). Per inciso, la funzione R(x) è una rozza approssimazione locale, poichè non riproduce le discontinuità finite di π(x) e, quindi, la distribuzione dei nmeri primi. Per ultimo, la circostanza 2 ci suggerisce un possibile ruolo svolto dalle funzioni di variabile complessa.
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.
Tags: approssimazione di Riemann, funzione Zeta di Riemann, legge di distribuzione dei numeri primi, numeri primi
Articoli correlati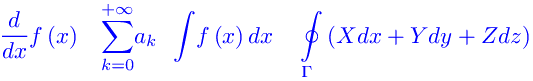


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan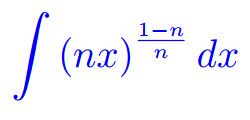 Eserciziario sugli integrali
Eserciziario sugli integrali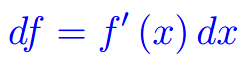 Differenziabilità
Differenziabilità 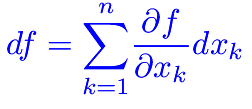 Differenziabilità (2)
Differenziabilità (2)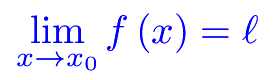 Esercizi sui limiti
Esercizi sui limiti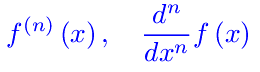 Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2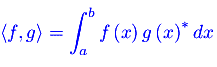 Analisi funzionale
Analisi funzionale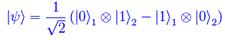 Entanglement quantistico
Entanglement quantistico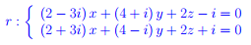 Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico