» Esercizi svolti di Matematica e Fisica

Annunci AdSense

[¯|¯] Rappresentazione parametrica regolare

Marzo 27th, 2017 | by Marcello Colozzo |

---

Definizione
Una rappresentazione parametrica

si dice regolare se:


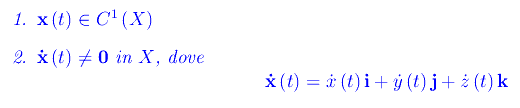
La condizione 1 richiede la continuità della funzione vettoriale x(t) e della sua derivata prima. La condizione 2, invece, implica l'assenza di zeri al finito della derivata prima. Risulta manifestamente:

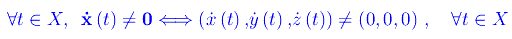
In altri termini, la condizione 2 ci dice che le derivate delle funzioni x(t),y(t),z(t) non si annullano mai per lo stesso valore del parametro t.









Ad esempio, consideriamo in R² la rappresentazione parametrica:

il cui codominio è la semicirconferenza Γ di centro l'origine e raggio unitario. Manifestamente x(t) è un elemento di C^oo}(X), per cui la condizione 1 è abbondantemente verificata. Anche la condizione 2 è soddisfatta. Infatti, la derivata prima della funzione vettoriale x(t) è:

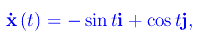
onde

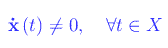
Ne consegue la regolarità della rappresentazione parametrica assegnata. Anticipiamo per ora che tale regolarità ci consente di tracciare la retta tangente a Γ in un suo generico punto come mostrato nell'animazione grafica di fig. 1.

---

---

Tags: curva, derivata, rappresentazione parametrica regolare, retta tangente

Articoli correlati