» Esercizi svolti di Matematica e Fisica

[¯|¯] Spezzata con vertici su una rosa a n=4 foglie

Nel programma precedente c'era un errore. Per inciso, Stan Wagon nel suo libro Guida a Mathematica utilizza un approccio differente. Precisamente, per generare la lista dei vertici invoca l'istruzione Range, esprimendo poi gli angoli in gradi anziché in radianti. Noi abbiamo utilizzato l'istruzione Table:

Ricordiamo che ξ(φ) è il vettore posizione di un punto variabile lungo la curva γ che in questo caso è una rosa a 4 foglie. Abbiamo poi assegnato l'attributo Listable: il kernel di Mathematica in modo da poter utilizzare come variabile una lista, come abbiamo fatto nel predetto codice che, tuttavia, presenta un errore in quanto ci siamo dimenticati di inserire nel costrutto di Table il passo d. Ricordiamo che in tal caso, Mathematica utilizza il valore di default che è 1. Stan Wagon nel suo libro scrive che un valore interessante per il passo d è 71° che corrisponde a circa 1.24 radianti. Noi abbiamo denotato tale valore con d_crit. Ripetendo la simulazione si ottiene la figura 1. L'ultimo "frammento" di codice per generare la figura 2 è:

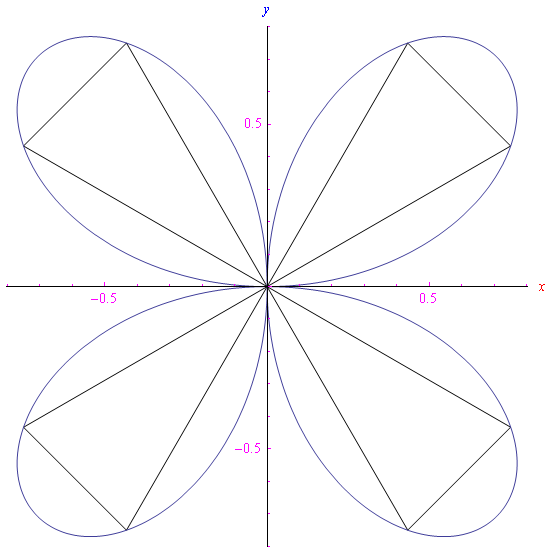
Esistono, poi, particolari valori del passo d per i quali la spezzata termina "prematuramente" nel senso che dopo un assegnato numero di passi ritorna nell'origine, come mostrato nella figura 3, dove N=460 e il passo è d=20 d_crit. Più in generale, ci aspettiamo "ritorni prematuri" per d=r* d_crit, dove q è un numero reale assegnato. Ad esempio, per r=10:

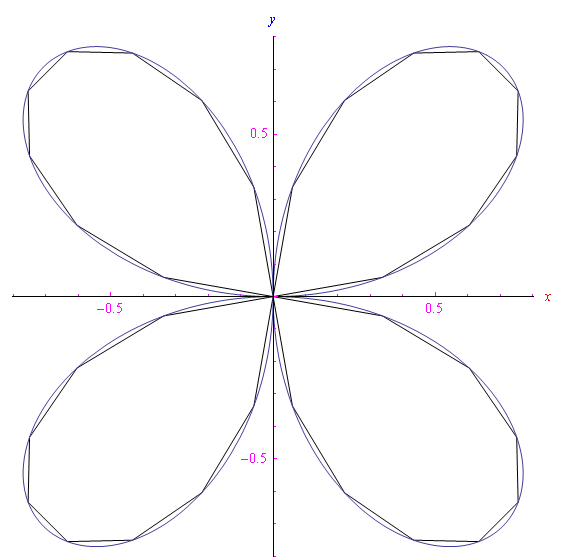
Per r=30

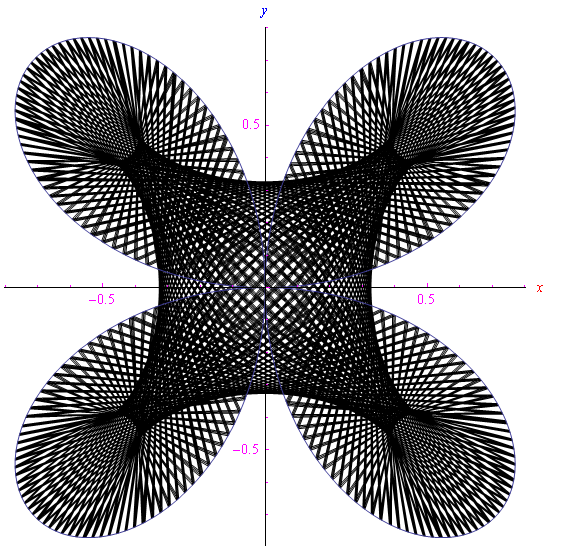
Per r=1/sqrt(2) otteniamo:

Tags: approssimazione lineare, coordinate polari, curva piana, Mathematica, rosa a n foglie