[¯|¯] Campi non semplicemente connessi e integrabilità di forme differenziali
martedì, Novembre 8th, 2016
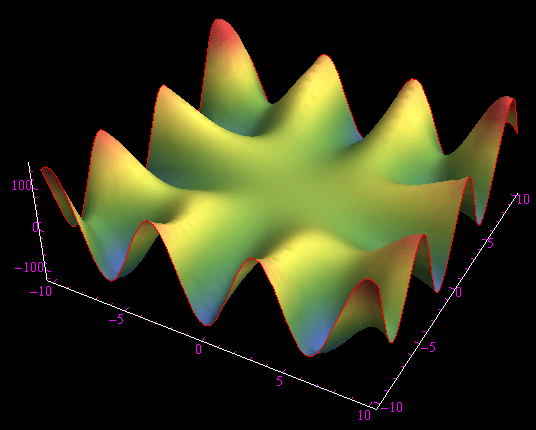
Fig. 1. Andamento del potenziale del campo vettoriale assegnato. Si noti la singolarità per x=1
Nell'esercizio precedente abbiamo esaminato il caso dell'integrabilità di una forma differenziale lineare definita in un campo semplicemente connesso. Nell'esercizio proposto (e risolto) il campo di esistenza non è connesso e a più forte ragione, non è semplicemente connesso. Quindi se vogliamo applicare le condizioni (necessarie) di integrabilità, dobbiamo considerare la restrizione dei coefficienti della forma a una regione a connessione lineare semplice (o semplicemente connessa)
(altro…)
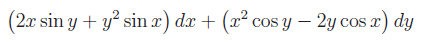
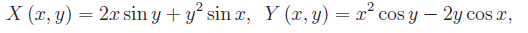
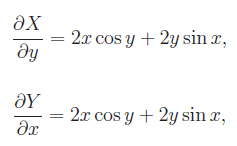
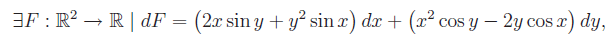
Congettura di Riemann
Trasformata discreta di Fourier
Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier 
Infinitesimi ed infiniti
Limiti notevoli
Punti di discontinuità
Misura di Peano Jordan
Eserciziario sugli integrali
Differenziabilità 
Differenziabilità (2)
Esercizi sui limiti
Appunti sulle derivate
Studio della funzione
Esercizi sugli integrali indefiniti
Algebra lineare
Analisi Matematica 2
Analisi funzionale
Entanglement quantistico
Spazio complesso
Biliardo di Novikov
Intro alla Meccanica quantistica
Entanglement Quantistico
