» Esercizi svolti di Matematica e Fisica

Confronto tra infinitesimi

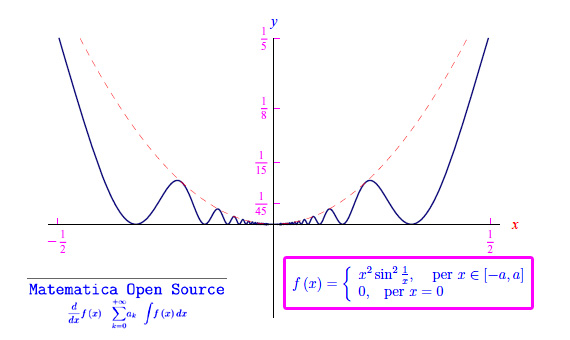
Il teorema enunciato in questo post, va rivisto in quanto è stato trovato un controesempio.

Un ulteriore controesempio potrebbe essere dato dalla funzione f(x)=x^2*sin(1/x)^2 per x in un qualunque compatto [-a,a] incluso x=0 in quanto la funzione è ivi continua. Inoltre, la funzione è derivabile in x=0 anche se questo punto è una singolarità per la derivata prima (abbiamo già trattato questo problema). Qui il problema che si apre è che la derivata non è un infinitesimo in x=0 per la predetta non regolarità in tale punto. Le altre ipotesi del teorema sono verificate, e cioè f(x) non negativa e derivata nulla in x=0. Il teorema va corretto aggiungendo che la derivata seconda non deve annullarsi in x=0 e che la derivata prima deve essere ovunque in continua. In altri termini, f è di classe C^1.

Scarica il controesempio in pdf

Tags: confronto, infinitesimi, ordine