» Esercizi svolti di Matematica e Fisica

Confronto tra infinitesimi (teorema)

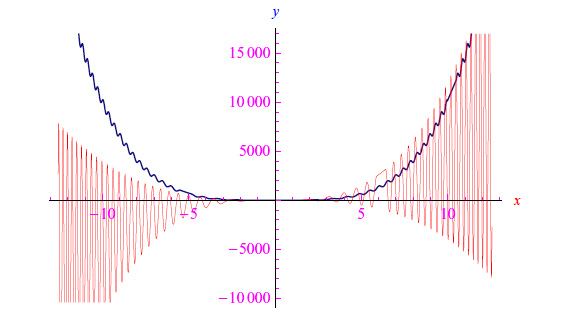
Sviluppando queste questo post, sembra necessario imporre la continuità della derivata seconda. In questo modo, applicando il noto teorema di De L'Hospital si rimuove la forma indeterminata 0/0 pervenendo a un limite che è finito se la derivata seconda è non nulla nel punto di accumulazione ξ (zero di f(x)) che stiamo considerando. Diversamente, il limite è infinito. Ciò implica che nel primo caso f(x)^1/2 e f'(x) sono infinitesimi dello stesso ordine, mentre nel secondo caso la derivata f'(x) è un infinitesimo di ordine superiore rispetto a f(x)^1/2.

Scarica la dimostrazione del teorema

Tags: confronto, infinitesimi, ordine, teoremi di De L'Hospital