[¯|¯] Vettori (Fisica 1 o Fisica Generale 1)

Dicembre 5th, 2019 | by Marcello Colozzo |

vettori,fisica 1, fisica generale 1 — **Fig. 1**

Esempio introduttivo

L'esempio proposto presuppone la conoscenza del calcolo vettoriale (quindi il lettore inesperto può passare direttamente al paragrafo successivo), ed espone in maniera chiara la straordinaria efficacia di tale paradigma. L'esempio è tratto dal famoso libro Halliday-Resnick; la soluzione è nostra.
Una squadriglia di boy-scout è rimasta bloccata in mezzo alla foresta, lontana dal suo attendamento (fig. 1). Basandosi sulle loro osservazioni, gli esploratori sanno di trovarsi a 2.0km di distanza dalle tende nella direzione che forma un angolo di 30° verso ovest rispetto al nord. Essi sanno anche che il loro attendamento è piantato a 3.0km di distanza dal campo base nella direzione che forma un angolo di 45° verso est rispetto al nord. Per ottenere soccorso devono comunicare via radio al campo base il luogo in cui si trovano. Come possono definire la loro posizione rispetto al campo base?

Soluzione

Questo esercizio si risolve facilmente con l'algebra vettoriale. Innanzitutto fissiamo un riferimento cartesiano ortogonale R(Oxyz) con l'origine nel campo base, e con gli assi coordinati orientati verso Est e Nord, rispettivamente (fig. 1). Il problema consiste nel determinare il vettore r che definisce la posizione dei boy-scout rispetto al campo base. Risulta:

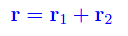
La formula appena scritta è un'equazione vettoriale che può essere proiettata sugli assi coordinati, ossia scritta componente per componente:

essendo (r_1x,r_1y) le componenti cartesiane del vettore r₁, mentre la coppia ordinata (r_2x,r_2y) definisce le componenti del vettore r₂. Dalla fig. 1

Passiamo al vettore r₂

Sostituendo questi dati nel precedente sistema di equazioni:

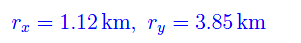
A questo punto non dobbiamo fare altro che calcolare modulo e direzione del vettore r:

Conclusione: i boy scout possono comunicare via radio la loro posizione, asserendo che si trovano a 4.0km dal campo base, nella direzione che forma un angolo di 73°46'.8 verso est rispetto al nord.">

Grandezze scalari e grandezze vettoriali

In Fisica alcune grandezze sono univocamente determinate da un numero reale che esprime il rapporto tra il valore della grandezza e una fissata unità di misura. Altre grandezze, invece, necessitano di ulteriori parametri. Questa prima e approssimata classificazione, suggerisce la seguente definizione:
Definizione
Si dicono grandezze scalari o semplicemente scalari, tutte e sole le grandezze fisiche univocamente determinate da un numero reale dato dal rapporto tra il valore della grandezza e una fissata unità di misura.
Esempi di grandezze scalari: temperatura, pressione, energia. Anche grandezze fondamentali quali lunghezza e tempo (intervalli di tempo) sono grandezze scalari. Nella dinamica del punto materiale incontreremo un'importante grandezza scalare: la massa.
Per quanto precede, esistono grandezze che non sono univocamente determinate dall'"ampiezza numerica". Si pensi ad esempio, allo spostamento di un corpo: una locuzione del tipo "il corpo si è spostato di 10 metri", è del tutto insufficiente per determinare l'effettivo spostamento, giacché occorre definire la direzione orientata secondo cui avviene lo spostamento medesimo. Quindi, accanto al numero che esprime l'ampiezza, vale a dire 10 metri, occorre specificare la direzione e il verso.
Generalizzando, possiamo dire che molti enti fisici sono rappresentati da particolari enti geometrici caratterizzati da una lunghezza ovvero un'ampiezza, e da una direzione orientata.
Definizione
Tali enti si dicono vettori e le grandezze rappresentate, grandezze vettoriali.
Un vettore è dunque rappresentato da un segmento orientato, la cuiu lunghezza esprime l'ampiezza della grandezza fisica (riispetto a una unità di misura). Si badi che tale definizione può essere fuorviante, poiché un vettore costituisce ciò che in matematica si chiama classe di equivalenza. Detto in altro modo, si definisce dapprima una cosiddetta relazione di equipollenza tra segmenti orientati appartenenti allo spazio ordinario (ovvero l'usuale spazio euclideo tridimensionale). Due segmenti orientati AB e CD si dicono equipollenti se oltre ad avere la medesima lunghezza, sono paralleli e concordi. Ne consegue che un vettore è l'elemento che accomuna un insieme di segmenti equipollenti
Un qualunque segmento dell'insieme rappresenta, dunque, il medesimo vettore come illustrato in figura:

La possibilità di prendere ad arbitrio uno dei predetti segmenti, si esprime dicendo che v è un vettore libero. Tuttavia in Fisica si presenta spesso la necessità di specificare il punto di applicazione di un vettore. In tal caso siamo in presenza di un nuovo ente geometrico denominato vettore applicato.
Per quanto riguarda la notazione, un vettore (libero o applicato) viene indicato con una lettera (minuscola o maiuscola) grassettata o soprasegnata da una freccia. Ad esempio

Salvo avviso contrario, in queste lezioni utilizzeremo la notazione grassettata.

Campo scalare e campo vettoriale

Le nozioni di campo scalare e campo vettoriale, sono spiegate in maniera esaustiva in appunti.

Algebra vettoriale. Rappresentazione cartesiana di un vettore

Dall'Algebra lineare
sappiamo che l'insieme R³ delle terne ordinate di numeri reali, può essere strutturato come spazio vettoriale reale attraverso l'introduzione di due leggi di composizione: addizione di vettori e moltiplicazione di uno scalare per un vettore. Qui il termine vettore si riferisce a un elemento di R³ ovvero a una terna ordinata di numeri reali. Tale definizione riproduce quella stabilita nei numeri precedenti. Infatti, istituendo un riferimento cartesiano ortogonale R(Oxyz) come in figira:

definiamo innanzitutto:

Definizione
Un versore è un vettore di modulo unitario. Un tale ente viene a volte denominato vettore unitario.
Un versore definisce una direzione orientata dello spazio ordinario. Ad esempio, assegnata una retta orientata r, il versore di r è un vettore di modulo unitario parallelo e concorde a r. Nel caso speciale degli assi coordinati x,y,z del riferimento R, i corrispondenti versori vengono solitamente denotati con i,j,k.
Ciò premesso, la legge di composizione addizione di vettori si realizza graficamente attraverso la ben nota regola del parallelogramma

Proiettando ortogonalmente il vettore v sugli assi coordinati, e denotando con v_x,v_y,v_z le misure relative dei segmenti intercettati sui predetti assi, è facile persuadersi che

La terna ordinata (v_x,v_y,v_z) definisce le componenti cartesiane del vettore v rispetto al riferimento cartesiano R(Oxyz).
Da ciò segue l'identificazione di un vettore dello spazio ordinario con una terna di numeri reali, come anticipato in precedenza. Come è noto, sono soddisfatti i seguenti assiomi per ciò che riguarda la legge di composizione addizione di vettori:

Gli assiomi verificati dalla legge di composizione moltiplicazione di uno scalare per un vettore, sono: