» Esercizi svolti di Matematica e Fisica

[¯|¯] Rette caratteristiche dell'equazione della corda vibrante

Ottobre 18th, 2018 | by Marcello Colozzo |

Riscriviamo la soluzione di D'Alembert nella forma stabilita nei post precedenti link 1 e link 2

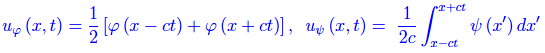
Si tratta ovviamente di due funzioni reali delle variabili reali x,t definite su tutto R².

Consideriamo, quindi, il piano cartesiano (Oxt), prendendo ad arbitrio il punto P₀(x₀,t₀) per poi determinare il valore ivi assunto dalle predette funzioni. Cioè

e

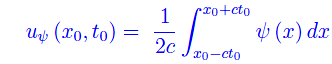
da cui vediamo che u_P0 è la media artimetica dei valori assunti dal campo scalare φ(x) nei punti dell'asse x di ascissa x₀-ct e x₀-ct, rispettivamente. Prendiamo ora le rette:

---

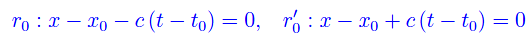
Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

---

La retta r₀ interseca l'asse x nel punto x₀-ct₀, mentre l'intersezione di r'₀ con l'asse x è ₀+ct₀, come illustrato in figura:

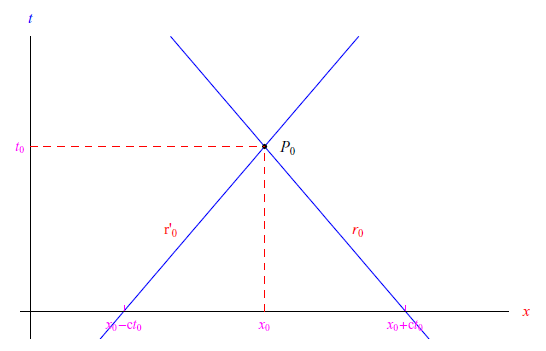
Inoltre, le due rette si intersecano nel punto P₀. DAll'altra formula segue, invece, che il valore assunto da u_&pshi; in P₀ è l'integrale esteso da x₀-ct₀ a x₀+ct₀ della funzione &pshi;(x), diviso per 2c.
Dall'arbitrarietà del punto P₀ segue l'esistenza di due fasci di rette parallele:

Per quanto precede

tale che (r₀,r'₀) trasporta l'informazione contenuta nei dati iniziali, giacché le funzioni φ(x) e ψ(x) individuano tali dati.
Definizione
Le rette

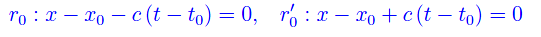
si dicono rette caratteristiche dell'equazione differenziale

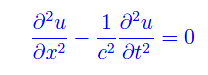
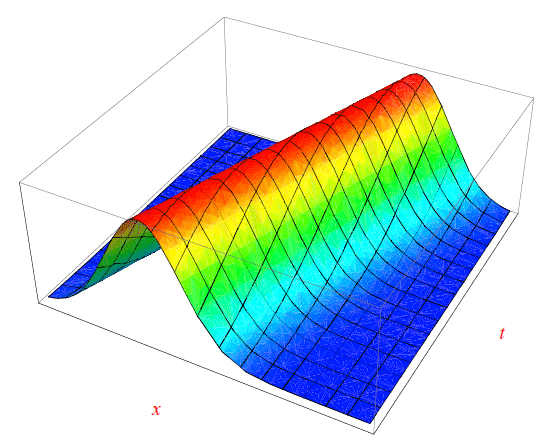
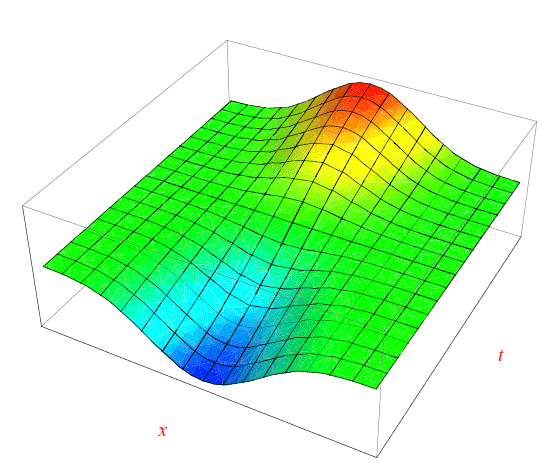
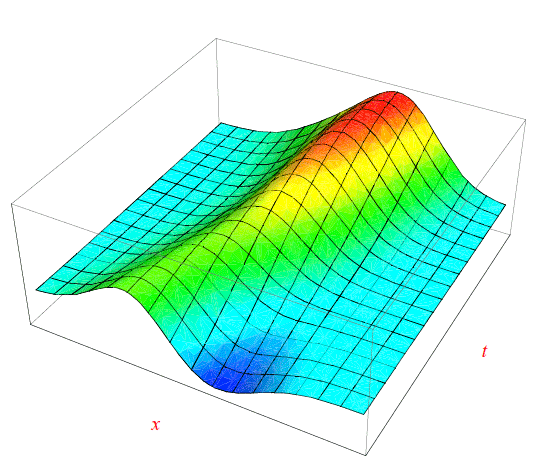
Concludiamo questo numero, riportando i grafici delle funzioni u_φ(x,t),u_ψ(x,t) e u_φ(x,t)+u_ψ(x,t) nelle figure seguenti

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

---

Tags: equazione della corda vibrante, equazioni differenziali alle derivate parziali, rette caratteristiche

Articoli correlati