[¯|¯] Riepilogo parziale sull'insieme di Cantor
Aprile 9th, 2017 | by Marcello Colozzo |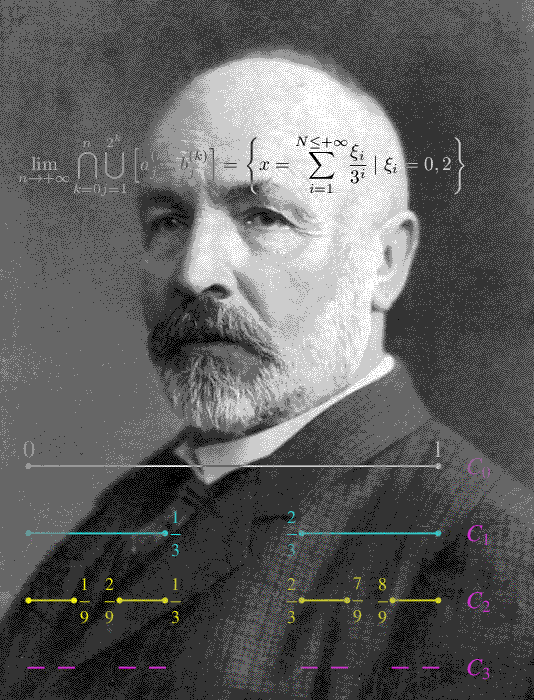
Per non perderci per strada cerchiamo di riepilogare i risultati raggiunti. Siamo partiti dall'insieme C0:
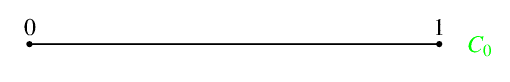
ovvero dall'intervallo [0,1] o ciò che è lo stesso, il segmento i cui estremi hanno ascissa 0 e 1, appartenente alla retta reale.
Dividiamo tale segmento in tre parti di pari lunghezza ossia in tre segmenti di lunghezza 1/3, dopodiché rimuoviamo il segmento centrale e chiamiamo C1 l'insieme ottenuto (che è l'unione di due intervalli disgiunti), come mostrato in figura:
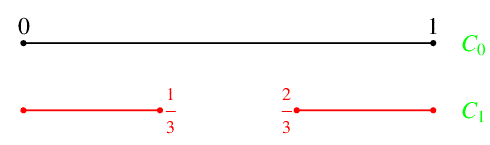
Applichiamo lo stesso procedimento ai segmenti che compongono C1, ottenendo quattro segmenti ciascuno di lunghezza 1/9, come vediamo dalla figura:

Una suddivisione ulteriore restituisce otto segmenti ciascuno di lunghezza 1/27, come appare dalla figura:

Ripetendo un numero infinito di volte tale operazione di suddivisione, otteniamo infiniti segmenti di lunghezza infinitesima, giacché la k-esima suddivisione restituisce 2k segmenti ciascuno di lunghezza 3-k Poniamo

per cui

Per quanto visto
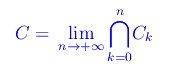
Ma
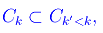
onde
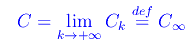
In altri termini, l'insieme di Cantor è "ciò che rimane" dopo le infinite suddivisioni, i.e. infiniti segmenti di lunghezza infinitesima. D'altra parte, per il teorema dimostrato in precedenza, si ha che "ciò che rimane" è il sottoinsieme di [0,1] i cui elementi non contengono l'1 nella rappresentazione in base 3:
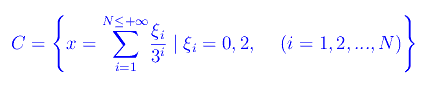
***
Prendiamo x0 appartenente all'insieme di Cantor la cui espansione ternaria è
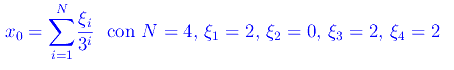
Quindi
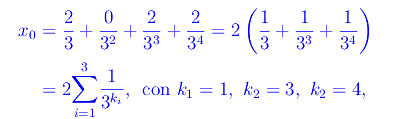
ovvero
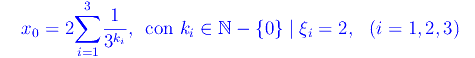
Abbiamo dunque trovato due espansioni ternarie distinte dello stesso elemento x0 dell'insieme di Cantor. Tale proprietà si generalizza a ogni elemento del predetto insieme, cosicché:
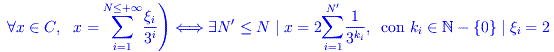
Infine osserviamo che
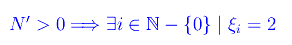
Viceversa

Sostienici
No TweetBacks yet. (Be the first to Tweet this post)
Tags: insieme di cantor, insieme perfetto, insieme ricorsivo, misurabilità dell'insieme di cantor
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











