[¯|¯] Caratterizzazione dell'insieme di Cantor attraverso un importante teorema
Aprile 8th, 2017 | by Marcello Colozzo |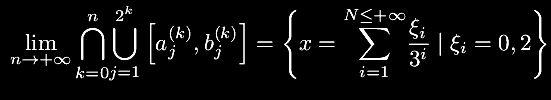
Introduciamo una particolare notazione per gli estremi degli intervalli che compongono la k-esima iterazione che porta alla definzione dell'insieme di Cantor. A tale scopo scriviamo:
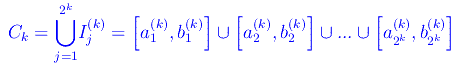
Denotiamo con A(k) l'insieme i cui elementi sono gli estremi sinistri dei singoli intervalli I(k)j, cioè
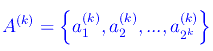
e con B(k) l'insieme i cui elementi sono gli estremi destri dei predetti intervalli:
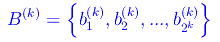
Ad esempio, per k=1
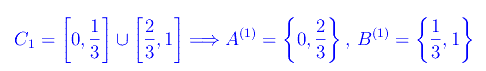
Per k=2
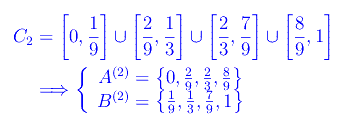
Per maggiore chiarezza, vedere la figura:
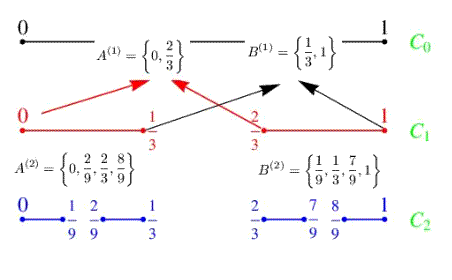
La k-esima iterazione definisce altri due sottoinsiemi di [0,1]:s
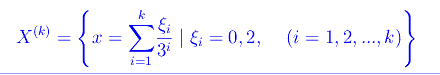
Cioè X(k) è l'insieme di tutti e soli i punti la cui espansione ternaria (i.e. in base 3) è di ordine k e non contiene 1.
Osservazione
In genere un'espansione in base b>1 di un reale x in (0,1) è del tipo
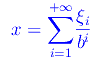
Si dice, invece, di ordine k, se la predetta serie è troncata al k-esimo termine:
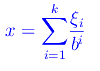
L'altro insieme è
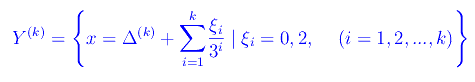
Ricordiamo che Δ(k) è l'ampiezza del singolo intervallo che compone la k-esima iterazione Ck:
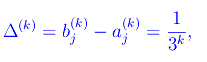
per cui i punti di Y(k) sono i punti di X(k) traslati di Δ(k) nel verso positivo dell'asse x. Inoltre, dalla proposizione dimostrata in una lezione precedente:
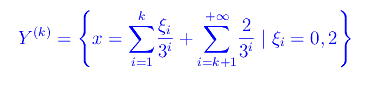
Per k=1
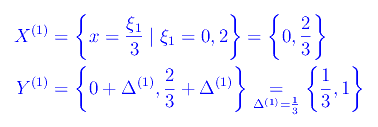
Cioè
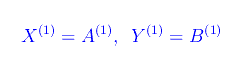
Per k=2
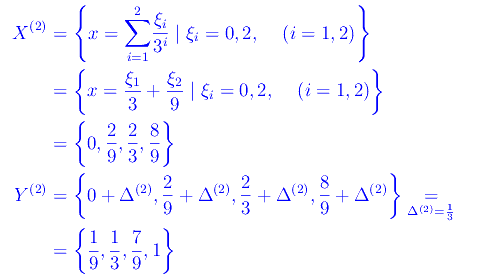
Cioè
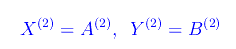
Procedendo per induzione:
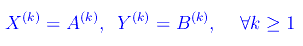
Dopo questa lunga premessa, definiamo l'insieme:
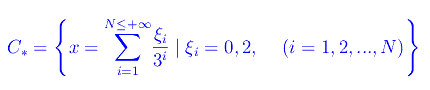
A differenza di X(k) che contiene l'espansione ternaria di ordine k dei reali in (0,1) priva dell'intero 1, l'insieme C* è la totalità delle espansioni reali (quindi di ordine arbitrario) di x in (0,1) e tale espansione non contiene l'intero 1. Dimostriamo il teorema
Teorema
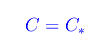
Dimostrazione
Si tratta di dimostrare
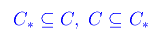
Inclusione diretta
Ricordiamo che l'insieme di Cantor è per definizione:
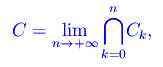
ed è un insieme chiuso per cui
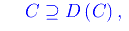
essendo D(C) il derivato di C, i.e. l'insieme dei punti di accumulazione per C. Quindi per dimostrare l'inclusione diretta occorre e basta provare che ogni elemento di C* è di accumulazione per C. Intanto vediamo che per come abbiamo definito C*, i suoi elementi sono tutti e soli aj(k) per qualunque k. Cioè
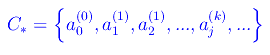
Ma
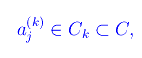
quindi
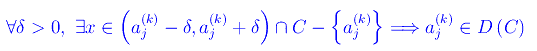
Segue
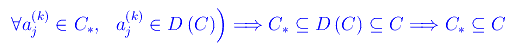
Inclusione inversa
Osserviamo che
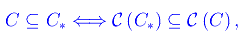
dove il simbolo calligrafico denota il complementare in [0,1]. Evidentemente
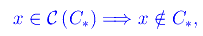
cosicché nell'espansione ternaria di x, l'1 compare almeno una volta. Più precisamentes
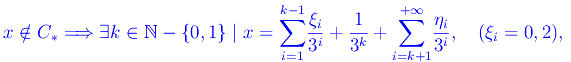
Riguardo a ηi iniziamo con il dimostrare
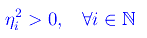
Procediamo per assurdo
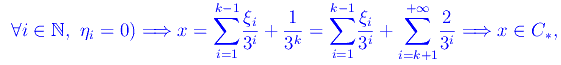
che contraddice l'ipotesi. Una seconda proprietà dei termini ηi è
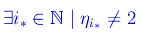
Procedendo per assurdo
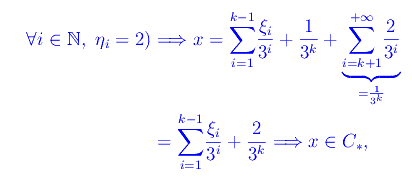
che contraddice l'ipotesi. Si conclude che
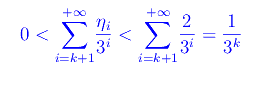
Ma
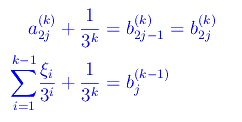
Segue
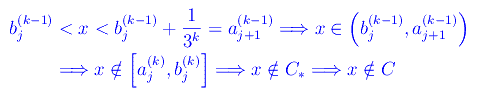
Cioè
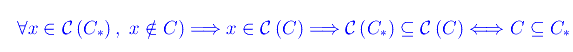
Sostienici
Tags: insieme di cantor, insieme perfetto, insieme ricorsivo, misurabilità dell'insieme di cantor
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











