[¯|¯] Sistemi di equazioni lineari con Mathematica. I comandi LinearSolve e Reduce

Dicembre 18th, 2016 | by Marcello Colozzo |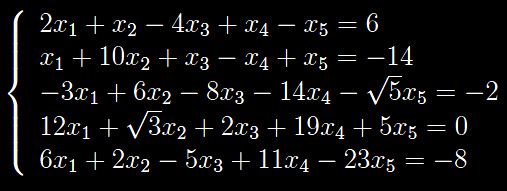

Mathematica risolve sistemi di equazioni lineari attraverso l'istruzione LinearSolve, la cui sintassi richiede la scrittura matriciale del sistema, cioè del tipo AX=B, dove A=(a_ik) è la matrice dei coefficienti, mentre X e B sono rispettivamente il vettore colonna delle incognite e il vettore colonna dei termini noti. Ad esempio, nel caso di un sistema di 3 equazioni nelle 3 incognite x,y,z, si ha:

sistemi di equazioni lineari, mathematica,linearsolve,reduce,nullspace

sistemi di equazioni lineari, mathematica,linearsolve,reduce,nullspace
Verifica

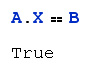
sistemi di equazioni lineari, mathematica,linearsolve,reduce,nullspace
Proviamo con un sistema omogeneo:

Attenzione: nel caso omogeneo, l'istruzione LinearSolve restituisce solo la soluzione banale, ignorando le eventuali soluzioni non nulle (le cosiddette soluzioni proprie o autosoluzioni). Nel caso omogeneo bisogna utilizzare l'istruzione NullSpace che restituisce una base dello spazio nullo della matrice dei coefficienti:

sistemi di equazioni lineari, mathematica,linearsolve,reduce,nullspace
cioè il sottospazio improprio o nullo, per cui il sistema assegnato ammette la sola soluzione banale. Ciò è confermato dalla determinazione del rango di A (che in questo caso è uguale al numero delle incognite):