» Esercizi svolti di Matematica e Fisica

Zeri semplici dell'energia potenziale (in funzione dell'ascissa)

venerdì, Novembre 13th, 2020

---

Nei casi di interesse fisico, la regione accessibile Λ(E) è l'unione di un numero finito di intervalli. Ad esempio, per una particella soggetta a una forza elastica con costante k=2 (in unità adimensionali), l'energia potenziale è

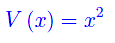
Per m=2 (massa della particella) e E=1 (energia meccanica totale), si ha

per cui la regione accessibile è [-1,1], i cui estremi sono zeri semplici per f(x):

Gli zeri semplici sono, dunque, i punti di frontiera della zona accessibile. Mostriamo che essi sono raggiunti in un tempo finito.

Corollario

(altro…)

---

Posted in Fisica generale 1, Meccanica analitica, meccanica razionale | No Comments »