Forze centripete e centrifughe

Giugno 9th, 2020 | by Marcello Colozzo |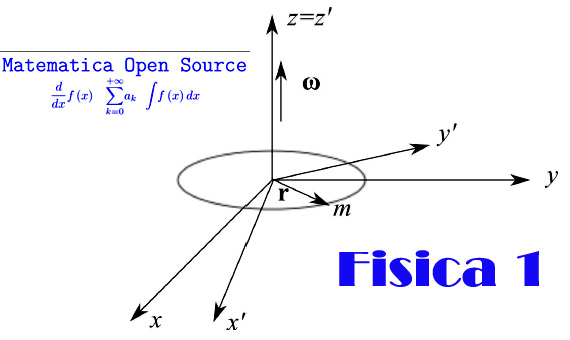

forza centripeta,forza centrifuga,sistema di riferimento non inerziale — **Fig. 1**

Nel piano coordinato xy di un sistema di riferimento inerziale K(Oxyz), una pallina di massa m è vincolata a muoversi lungo una circonferenza di centro l'origine O e raggio r (il vincolo è realizzato da un filo inestensibile e di massa nulla), come illustrato in figura:

Trascuriamo l'attrito e supponiamo che il moto sia circolare uniforme. Dalla cinematica del punto materiale sappiamo che l'accelerazione della pallina è puramente normale (o centripeta):

dove v è la velocità scalare (costante) e n è il versore della normale alla traiettoria:

avendo introdotto il vettore posizione r nel piano coordinato in cui si svolge il moto (fig. 1). Introducendo la velocità angolare

si ha

Cioè

Per il secondo principio della dinamica, la pallina è soggetta a una forza

che chiamiamo forza centripeta. Consideriamo ora un secondo sistema di riferimento K'(Ox'y'z') solidale alla pallina. Più precisamente, nell'istante iniziale t=0 (pallina ferma) è K sovrapposto a K', mentre a t > 0 K' ruota attorno all'asse z di K con velocità angolare ω. È chiaro che K' non è un sistema inerziale in quanto non compie un moto di traslazione uniforme (rispetto a K). Dal momento che K' ruota con velocità angolare ω, un qualunque osservatore Ω fermo in K, vedrà la pallina occupare sempre la stessa posizione. Ne consegue (in virtù del secondo principio della dinamica) che per Ω è F=0, essendo F il risultante delle forze applicate alla pallina. Immaginiamo ora la seguente configurazione sperimentale: a un istante t₁ > 0 l'osservatore Ω taglia il filo che realizza il vincolo. A t > t₁, Ω vedrà la pallina compiere un moto rettilineo uniformemente accelerato nella direzione del filo e verso l'esterno della circonferenza di centro l'origine e raggio r (lunghezza del filo). Come potrebbe Ω calcolare la forza agente responsabile del moto accelerato della pallina? Il metodo più veloce consiste nel determinare la forza uguale e contraria applicata alla pallina nell'istante t₁ affinché la pallina medesima resti in quiete. Ω scopririà allora, che tale forza opposta è proprio la forza centripeta stabilita dall'osservatore inerziale:

Ne consegue che la forza incognita è

e si chiama forza centrifuga. Si tratta di una forza fittizia (cioè non reale) la cui introduzione è necessaria per l'applicazione del secondo principio della dinamica. Detto in altro modo, la predetta forza fittizia tiene conto della dinamica rotazionale del sistema di riferimento K' che Ω mai potrebbe rilevare in quanto solidale a K'.
Notiamo infine che si perviene allo stesso risultato applicando il principio dei moti relativi: