La funzione di Airy e il neutrone in caduta libera
martedì, Marzo 16th, 2021
Se il neutrone fosse un oggetto classico, il problema della caduta libera si risolverebbe al volo. Infatti, orientando un asse x verso l'alto, si ha che il potenziale del campo di gravità è

dove m è la massa del neutrone e g l'accelerazione di gravità. Si noti che abbiamo posto lo zero del potenziale in x=0 (suolo). Applicando il secondo principio della dinamica si perviene all'equazione differenziale del moto:

che assieme alle condizioni iniziali x(0)=x0 e d/dt(x(t))=0 (per t=0) restituisce l'unica soluzione

che ci consente di calcolare l'istante di arrivo al suolo:

Schematizzando il suolo come una superficie infinitamente dura, si ha un urto elastico ed è facile determinare la dinamica del processo a tutti i tempi. Sfortunatamente, il neutrone è un oggetto quantistico per cui non è possibile assegnare una condizione iniziale di quella vista prima giacché violerebbe il principio di indeterminazione di Heisenberg. La Meccanica quantistica ci dice che dobbiamo risolvere lo spettro dell'operatore hamiltoniano:

Dal momento che il suolo è una superficie infinitamente dura, si ha:

Per un assegnato valore E=mgx0 dell'energia, la regione classicamente accessibile

Ne segue che lo spettro dell'hamiltoniano è puramente discreto. Abbiamo, dunque, solo stati legati. Per determinare lo spettro dobbiamo risolvere l'equazione agli autovalori:

cioè integrare l'equazione differenziale del secondo ordine (equazione di Schrödinger non dipendente dal tempo)

Con le condizioni al contorno:

È preferibile passare al dominio degli impulsi. Come è noto, ciò equivale ad eseguire la trasformata di Fourier giacché le autofunzioni dell'energia nel predetto dominio sono:

Eseguendo la trasformata di Fourier delle funzioni che compaiono nell'equazione di Schrödinger, otteniamo la medesima equazione scritta nel dominio degli impulsi:

che è del primo ordine e a variabili separabili:

da cui

Segue

(altro…)


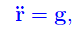




 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











