« Previous Entries
Next Entries »

[¯|¯] Esercizio sui funzionali lineari (spazio duale)

giovedì, Novembre 24th, 2016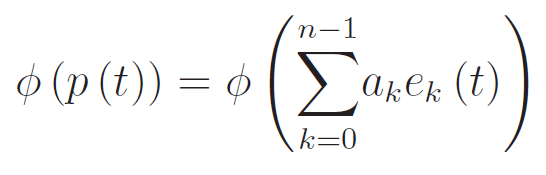

spazio duale,funzionale lineare,base duale,spazio vettoriale dei polinomi

Esercizio
Denotiamo con Pn-1[t] l'insieme dei polinomi di grado <=n-1, nell'indeterminata t e a coefficienti reali. Cioè:

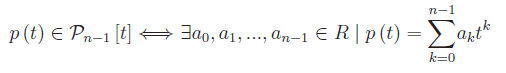
spazio duale,funzionale lineare,base duale,spazio vettoriale dei polinomi

  1. Mostrare che introducendo in Pn-1[t] le leggi di composizione:
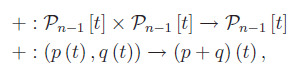
    spazio duale,funzionale lineare,base duale,spazio vettoriale dei polinomi

    così definita
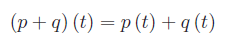
    spazio duale,funzionale lineare,base duale,spazio vettoriale dei polinomi

    e
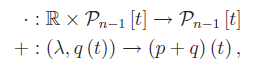
    spazio duale,funzionale lineare,base duale,spazio vettoriale dei polinomi

    così definita:
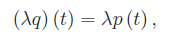
    spazio duale,funzionale lineare,base duale,spazio vettoriale dei polinomi

    l'insieme Pn-1[t] assume la struttura di spazio vettoriale sul campo reale.

    2. (altro…)



Posted in Algebra Lineare | No Comments »

[¯|¯] Base duale (di una base di uno spazio vettoriale)

mercoledì, Novembre 23rd, 2016

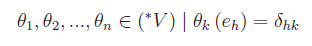
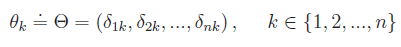
funzionale lineare,spazio duale,base duale,spazio vettoriale,sistema lineamente dipendente,sistema massimo linearmente indipendente


Consideriamo i funzionali lineari:

funzionale lineare,spazio duale,base duale,spazio vettoriale,sistema lineamente dipendente,sistema massimo linearmente indipendente

Riesce
funzionale lineare,spazio duale,base duale,spazio vettoriale,sistema lineamente dipendente,sistema massimo linearmente indipendente

Inoltre:

funzionale lineare,spazio duale,base duale,spazio vettoriale,sistema lineamente dipendente,sistema massimo linearmente indipendente

cioè
funzionale lineare,spazio duale,base duale,spazio vettoriale,sistema lineamente dipendente,sistema massimo linearmente indipendente

Ciò premesso, dimostriamo il teorema:
Teorema
{θk} è una base di *V.
Dimostrazione
Il sistema di vettori *Σ={θ1},...,θ2} è univocamente determinato dalle
funzionale lineare,spazio duale,base duale,spazio vettoriale,sistema lineamente dipendente,sistema massimo linearmente indipendente

(altro…)



Posted in Algebra Lineare | No Comments »

« Previous Entries
Next Entries »