[¯|¯] Funzioni con punti di discontinuità di prima specie
giovedì, Gennaio 12th, 2017
Fig. 1
Nell’esercizio precedente abbiamo visto che la funzione

ha in x = 1 un punto di discontinuità di prima specie, giacché:

La discontunuità `e dovuta alla presenza di |x-1|/(x-1) che può essere scritta come sgn(x - 1), dove sgn(·)
è la funzione signum:

Un’altra funzione che presenta punti di discontinuità di prima specie è arctan il cui argomento ha
una discontinuità di seconda specie. Più precisamente, consideriamo la funzione composta

con g(x) tale che

Segue

onde x0 è un punto di discontuinità di prima specie con salto s(x0)=π. Se invece

x0 è un punto di discontuinità eliminabile. Di seguito alcuni esempi.
Esempio 1
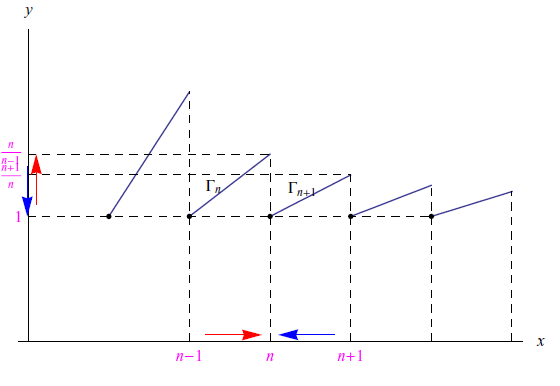
Studiamo il comportamento della funzione

in un intorno di x=1. Abbiamo

Il grafico è riportato in fig. 1.
Studiamo il comportamento della funzione

in un intorno di x=1. Abbiamo

per cui x=1 è un punto di discontuinità eliminabile.

Fig. 1
Studiamo il comportamento della funzione

in un intorno di x=1. Abbiamo


Fig. 1



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











