[¯|¯] Regolarità di una rappresentazione parametrica e iniettività locale
sabato, Marzo 25th, 2017
Fig. 1. Esempio di curva regolare dotata di punti multipli. Si tratta comunque di una curva "localmente semplice"
Nel post precedente abbiamo introdotto il concetto di "traiettoria" di un punto materiale rispetto a un'assegnata terna di riferimento K(Oxyz). Esaminiamo ora tale nozione dal punto di vista della Geometria differenziale.
Definizione
Una rappresentazione parametrica
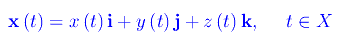
si dice regolare se:
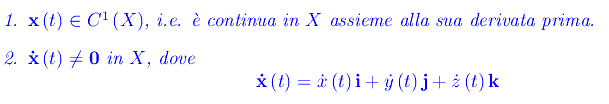
Una curva ammette infinite rappresentazioni parametriche. Ad esempio, consideriamo
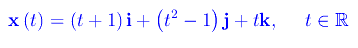
Eseguiamo il cambio di parametro:
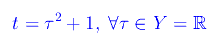
Risulta
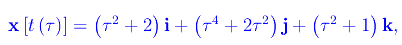
che definisce una nuova rappresentazione parametrica della stessa curva, ottenuta mediante una riparametrizzazione.
(altro…)
Congettura di Riemann
Trasformata discreta di Fourier
Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier 
Infinitesimi ed infiniti
Limiti notevoli
Punti di discontinuità
Misura di Peano Jordan
Eserciziario sugli integrali
Differenziabilità 
Differenziabilità (2)
Esercizi sui limiti
Appunti sulle derivate
Studio della funzione
Esercizi sugli integrali indefiniti
Algebra lineare
Analisi Matematica 2
Analisi funzionale
Entanglement quantistico
Spazio complesso
Biliardo di Novikov
Intro alla Meccanica quantistica
Entanglement Quantistico
