Osculating circle (Cerchio osculatore)

giovedì, Dicembre 3rd, 2020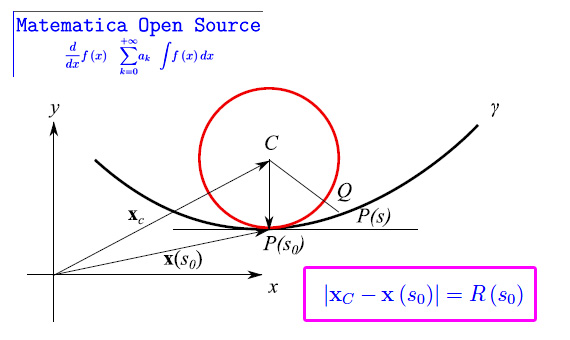

Quale è la migliore approssimazione a una curva in un intorno di un punto assegnato? La risposta più ovvia è la retta tangente, per un intorno sufficientemente piccolo. Ma qui vogliamo approssimarla in "modo curvilineo" (rozzamente parlando). Enunciamo e dimostriamo un teorema secondo cui la migliore approssimazione è un arco di circonferenza tangente alla curva nel punto dato, e avente raggio pari al raggio di curvatura (calcolato in quel punto). È il famoso cerchio osculatore, che generalizza la nozione di "osculazione", dal francese "baciarsi". Infatti, abbiamo studiato i punti di osculazione in una lezione precedente, anche se lì avevano una connotazione per così dire, negativa 😀 giacché ci si riferiva ai punti singolari di una curva.
PS. Sia chiaro, stiamo parlando di curve piane...

Scarica la dimostrazione del teorema in pdf
(altro…)

Posted in Geometria differenziale, Geometria II, Meccanica analitica | No Comments »

[¯|¯] Piano osculatore alla cubica sghemba

mercoledì, Settembre 27th, 2017

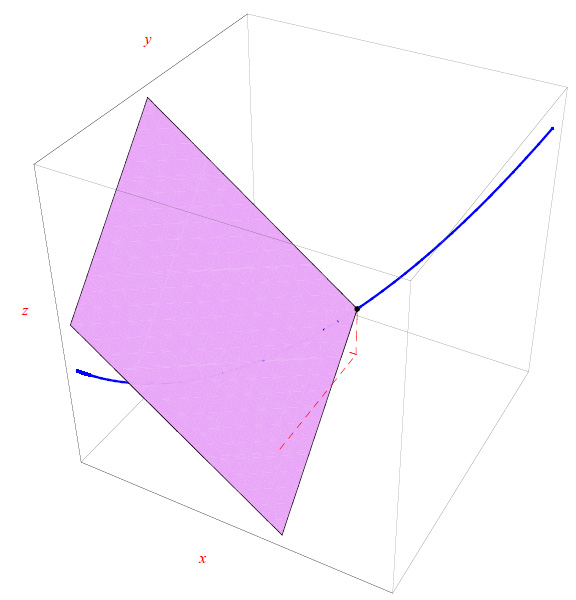
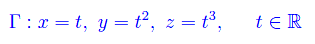
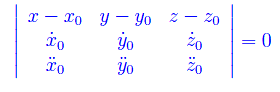
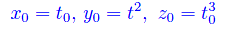
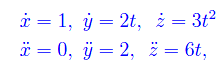
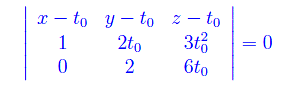
piano osculatore,cerchio osculatore,cubica sghemba

Nel post precedente abbiamo esaminato la nozione di piano osculatore e cerchio osculatore ad una assegnata curva regolare. Vediamo ora un esempio numerico offerto dalla determinazione del piano osculatore alla cubica sghemba: