» Esercizi svolti di Matematica e Fisica

[¯|¯] L'equazione di Thomas-Fermi nel paradigma della geometria differenziale

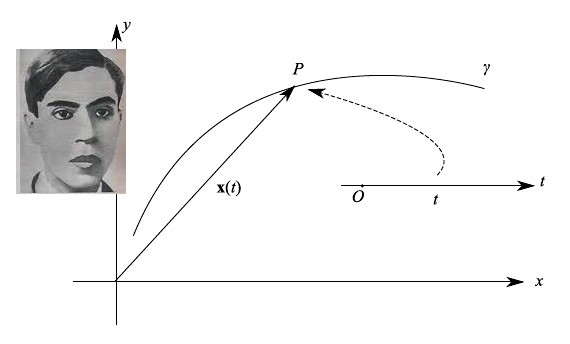
Potrebbe esserci un legame tra metodo utilizzato da Ettore Majorana per integrare la celebre equazione di Thomas-Fermi e la nozione di rappresentazione parametrica di una curva piana. Si parte passando ad una rappresentazione parametrica di una assegnata curva integrale di una equazione differenziale del secondo ordine non lineare ove non compare la derivata prima (ci stiamo riferendo a una particolare classe di equazioni differenziali a cui appartiene la Thomas-Fermi). Ovviamente non conosciamo la rappresentazione parametrica, però il punto di forza del metodo di Majorana sta nei seguenti punti: 1) una curva (regolare o meno) ammette infinite rappresentazioni parametriche; 2) solitamente si considerano in geometria differenziale, curve prive di punti multipli (ecco perché è importante il concetto di iniettività di una funzione vettoriale, e questo lo vedremo a breve anche a carattere locale).
(altro…)

Posted in Geometria differenziale | No Comments »

[¯|¯] La genesi dell'equazione di Thomas-Fermi

in questo handbook esaminiamo le ragioni fisiche spinsero Fermi ad elaborare l'omonimo modello di atomo pesante (cioè a molti elettroni), per poi giungere alla celebre equazione di Thomas-Fermi.
Argomenti:

1. Introduzione
2. L'energia di Fermi

(altro…)

Posted in Fisica Teorica, Meccanica Quantistica, Meccanica Statistica | No Comments »