Potenziale periodico. Bande di energia

Archive for the ‘Meccanica Quantistica’ Category

Potenziale periodico. Bande di energia

sabato, Aprile 9th, 2022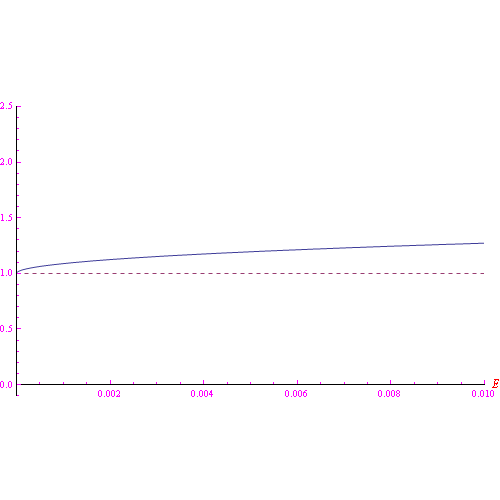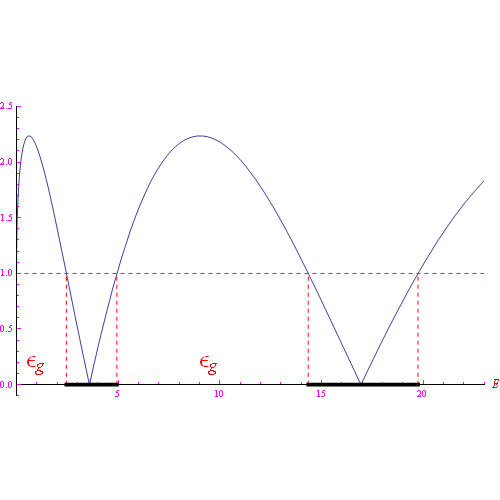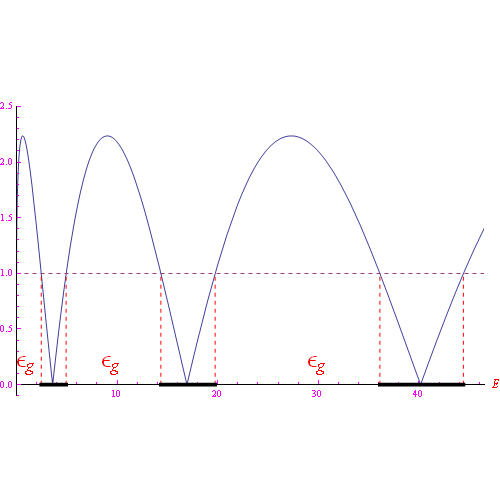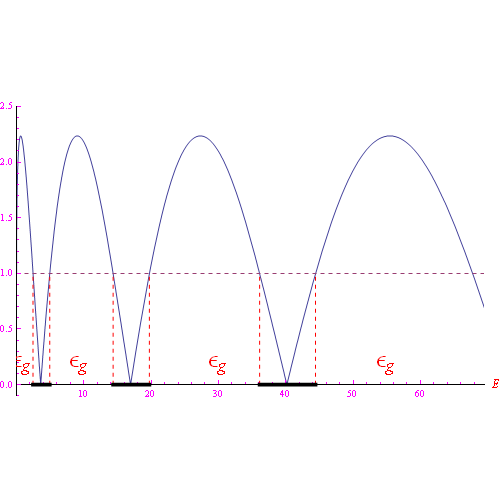

Risolviamo lo spettro dell'hamiltoniano di un sistema quantistico unidimensionale sottoposto a un potenziale periodico deltiforme:

Innanzitutto osserviamo che essendo infV(x)=0, lo spettro s(H) è puramente continuo ed è contenuto in (0,+8). Per il teorema di Bloch, le autofunzioni (improprie) dell'energia sono

dove v(x) è periodica di periodo a. Riesce, dunque

Posto ω=e^ika, si ha

per cui la u(x) è quasi periodica, nel senso che la funzione traslata u(x+a) differisce da u(x) per un numero complesso di modulo unitario. Suddividendo l'intervallo [0,2a] in I=[0,a] e II=[a,2a], si ha che in I l'equazione di Schrödinger stazionaria si scrive:

le cui soluzioni sono

con A,B costanti (complesse) di integrazione. Nella regione II sfruttiamo la proprietà di quasi periodicità:

Dobbiamo raccordare le soluzioni in x=a, imponendo la continuità di u(x), e una discontinuità finita della derivata prima (ciò è una conseguenza della presenza di una delta di Dirac, e si ricava facilmente prendendo l'integrale tra -ε e &epsilon di primo e secondo membro dell'eq. di Schrödinger, mandando poi &epsilon->0). Abbiamo

Tenendo delle equazioni scritte più sopra:

che è un sistema lineare omogeneo nelle incognite A,B. Affinché tale sistema ammetta soluzioni non banali, deve annullarsi il determinante della matrice dei coefficienti, da cui otteniamo facilmente

Quindi

Ma &eomga; è un numero complesso, per cui

che è una disequazione in E, e va risolta graficamente come in fig.

(altro…)

Posted in Meccanica Quantistica | No Comments »

Equazione di Schrödinger stazionaria per potenziali periodici

venerdì, Aprile 8th, 2022

equazione di Schrödinger stazionaria,potenziali periodici — **Fig. 1.**

A questa struttura cristallina dobbiamo introdurre gli "ingredienti fondamentali" ovvero particelle dotate di carica elettrica (elettroni/ioni). Tuttavia, l'aspetto fondamentale è la periodicità dell'energia potenziale in cui si muovono le predette particelle che per quanto precede, determina univocamente la struttura a bande dello spettro dell'hamiltoniano di singola particellla. Ed è così che si lavora in meccanica quantistica, vale a dire ci si focalizza sulla singola particella. L'origine di tale struttura a bande è intuitivamente ovvia. Ad esempio, per un problema studiato tempo addietro, avevamo visto che un'energia potenziale del tipo: