Un esempio di calcolo di Trasformata di Fourier
Febbraio 12th, 2016 | by Marcello Colozzo |
Proponiamo un semplice esempio in modo da capire i concetti fondamentali, che ci darà tra l'altro, la possibilità di calcolare la trasformata di Fourier a mano, cioè senza eseguire calcoli mostruosi. Supponiamo di avere una grandezza y variabile in funzione del tempo t, secondo la legge:
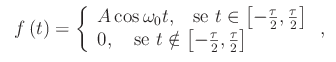
il cui grafico è:
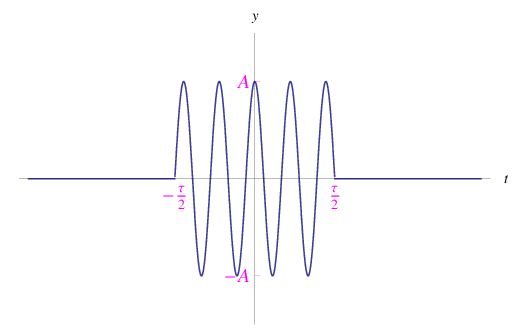
La grandezza f(t) non è periodica, ma è tuttavia esprimibile attraverso uno sviluppo in integrale di Fourier:
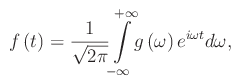
da cui vediamo che f(t) si esprime come una sovrapposizione lineare di infiniti termini monocromatici (o armonici o componenti di Fourier) di frequenza w variabile da -oo a +oo. La funzione g(w) è continua in (-oo,+oo) ed è tale che g(w)dw è l'ampiezza delle componenti di Fourier la cui frequenza è compresa tra w e w+dw. Ne consegue che la funzione g(w) è la densità spettrale nota anche come trasformata di Fourier della f(t).
Invertendo la relazione precedente:
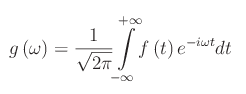
Per determinare la densità spettrale della funzione assegnata utilizziamo la notazione complessa:
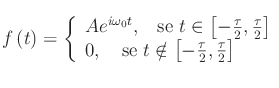
Calcolando l'integrale
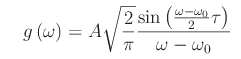
Vediamo che tale funzione è un'oscillazione sinusoidale modulata da (w-w0)^-1, come illustrato in figura:
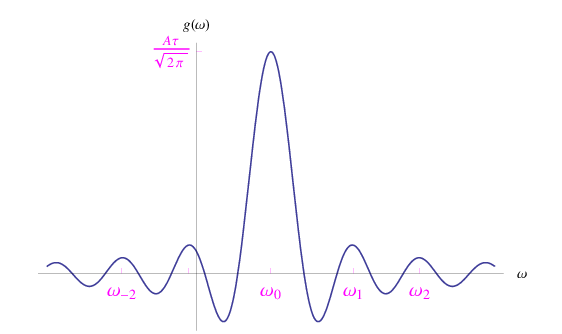
Il contributo dominante a f(t) proviene dalle componenti di Fourier con frequenza prossima a w0. D'altra parte, al crescere della durata del segnale, la densità spettrale diviene progressivamente più piccata intorno a w0, come mostrato dal grafico:
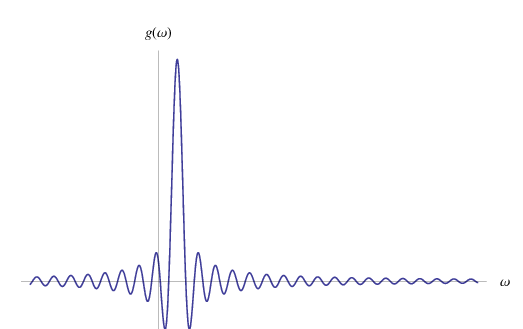
Al limite:
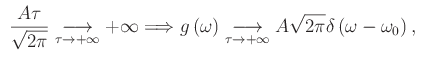
ritroviamo, in tal modo, la funzione delta di Dirac.
Inoltre:
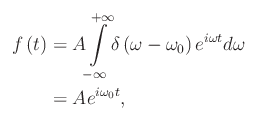
cioè la funzione assegnata (in notazione complessa) per t variabile ad -oo a +oo.
Viceversa, al diminuire di tau la distribuzione g(w) delle frequenze tende ad allargarsi, come mostrato dal grafico.

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: delta di dirac, densità spettrale, Trasformata di Fourier
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico









