[¯|¯] Forme indeterminate a gogo
Gennaio 15th, 2017 | by Marcello Colozzo |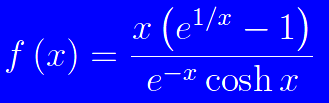
Fig. 1
Studiare il comportamento della funzione illustrata in fig. 1, agli estremi del suo campo di esistenza.
Soluzione
La funzione è definita in X=R-{0}, ed è istruttivo studiarne il segno.

onde la funzione è positiva in X. Studiamo il comportamento in un intorno del punto di accumulazione x=0. Precisamente:

L'indeterminazione è prodotta dal numeratore, per cui calcoliamo a parte
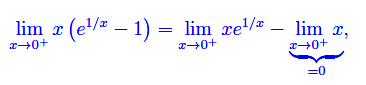
mentre
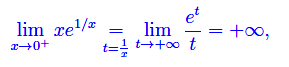
giacché et è, per t->+oo, un infinito di ordine infinitamente grande. Segue
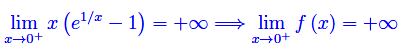
Ne consegue che l'asse y è asintoto verticale a destra per il grafico della funzione.
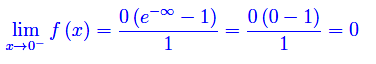
Dal momento che la funzione è positiva nel suo insieme di definizione, deve essere:
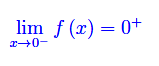
Calcoliamo
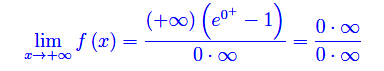
Cioè troviamo la forma indeterminata 0·oo sia a numeratore che a denominatore. Consideriamo l'espansione del coseno iperbolico in esponenziali, secondo la consueta definizione di coshx:
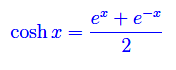
Segue

Siamo pertanto riusciti a rimuovere l'indeterminazione a denominatore. Calcoliamo a parte
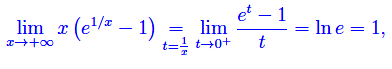
che è un caso particolare del limite fondamentale
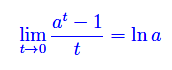
Pertanto
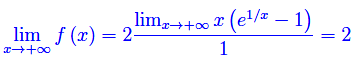
Da tale risultato emerge che la funzione è convergente per x->+oo e il limite vale 2. In termini geometrici, ciò implica che la retta y=2 è asintoto orizzontale a destra per il grafico della funzione. Ora calcoliamo
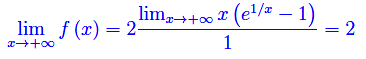
cioè nuovamente la forma indeterminata 0·oo sia a numeratore che a denominatore. Utilizzando l'artificio precedente:

Il limite a denominatore è +oo, mentre il limite a numeratore
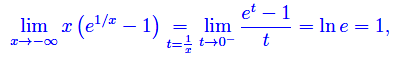
onde
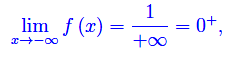
ovvero la funzione è infinitesima per x->-oos.
No TweetBacks yet. (Be the first to Tweet this post)
Tags: coseno iperbolico, esponenziale, Forme indeterminate, limiti
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











