» Esercizi svolti di Matematica e Fisica

Il limite quale punto di aderenza per il codominio di una funzione

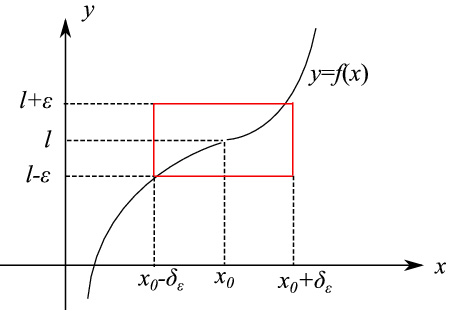
Proposizione
Se la funzione f:X->R è convergente in x0, il limite l è un punto di aderenza per il codominio f(X).

Dim.

L'asserto segue dalla definizione di limite:

illustrata in fig. 1.

Proposition
If the function f: X-> R is convergent at x0, the limit l is an adherence point for the codomain f (X).

Proof

The assertion follows from the definition of limit:

illustrated in fig. 1.

Tags: codominio, funzione, limite, punto di aderenza