[¯|¯] Può un proiettile colpire un bersaglio "prima" di essere sparato? (parte prima)

Gennaio 6th, 2019 | by Marcello Colozzo |

proiettile,trasformazioni galileiane,sistema di riferimento inerziale — .

In un poligono di tiro Bob spara un proiettile verso un bersaglio B, posto a distanza d sulla linea di tiro. Per semplicità, trascuriamo la forza di gravità e la resistenza dell'aria, per cui il proiettile si muove di moto rettilineo ed uniforme con velocità v. In questa schematizzazione, orientiamo un asse x con origine in O e direzione e verso secondo la linea di tiro:

Abbiamo, in tal modo, istituito un sistema di riferimento inerziale K in cuiu il tiratore e il bersaglio sono in quiete. Secondo l'orologio di Bob, il proiettile colpirà il bersaglio nell'istante

Alice è a bordo di un'auto che si muove di moto rettilineo uniforme con velocità V nella stessa direzione e verso del moto del proiettile. Abbiamo, dunque, un secondo sistema di riferimento inerzialae K'(O'x') con l'asse x' parallelo e concorde all'asse x, come illustrato in figura:

Trasformazioni galileiane

Dall'equazione precedente si ricava:

dove x è l'ascissa del proiettile all'istante t (rispetto a K), mentre x' è l'ascissa del proiettile rispetto a K'. Si noti che abbiamo tacitamente assunto t'=t, cioè gli orologi di Alice e Bob marcano lo stesso tempo o meglio, il tempo è invariante rispetto al cambiamento di sistema di riferimento inerziale. Possiamo, quindi scrivere:

che costituiscono le trasformazioni galileiane. In particolare:

qualunque sia V > 0.
Conclusione
Ogni punto del piano cartesiano x-ct è un evento che accade nel punto x e nell'istante t (rispetto a K).

Per un'infelice consuetudine un generico evento viene denotato attraverso le sue coordinate cartesiane (ct,x), dove è scambiata l'ascissa con l'ordinata. Per stabilire la successione degli eventi (rispetto a Bob) relativi alla traiettoria del proiettile, scriviamo l'equazione oraria del moto di quest'ultimo:

In figura è riportato il diagramma orario del proiettile nel riferimento inerziale K.

Il corrispondente diagramma spazio-temporale, è il diagramma cartesiano dell'inversa della funzione scritta precedentemente, onde:

riportato in figura:

Definizione
Tale luogo geometrico è la linea di universo del proiettile

La linea di universo è, dunque, il luogo geometrico degli eventi relativi a un assegnato processo. Le trasformazione galileiane non sono altro che le equazioni che ci fanno passare dalle coordinate spazio-temporali (ct,x) alle coordinate (ct',x'). Precisamente:

che sono banalmente invertibili:

Dalla seconda

che è l'equazione dell'asse ct' nel piano cartesiano ct-x. Allo stesso modo

è l'equazione dell'asse x' nel predetto piano cartesiano, come illustrato in figura:

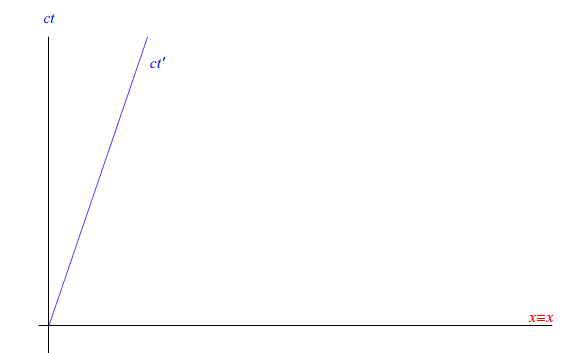
Vediamo, dunque, che mentre x e x' coincidono, l'asse ct' è inclinato rispetto all'asse ct di un angolo

Si noti che la coincidenza di x con x' esprime geometricamente l'identità t=t' ovvero l'invarianza della coordinata temporale ct per trasformazioni galileiane.

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

No TweetBacks yet. (Be the first to Tweet this post)