» Esercizi svolti di Matematica e Fisica

[¯|¯] Verso una numerizzazione dello spazio

Aprile 3rd, 2017 | by Marcello Colozzo |

---

Le difficoltà che si incontrano nello studio della Geometria differenziale e più in generale della Topologia, sono a nostro avviso riconducibili a una difficile visualizzazione dei concetti esposti. Fino a quando si lavora con Enti geometrici del tipo punto, curva, superficie, etc, la nostra percezione visiva ci aiuta a raggiungere una comprensione profonda di tali oggetti. La Topologia, invece, astrae da tali Enti per magari riconsiderarli come caso particolare, ricostruendo efficacemente i risultati dell'Analisi. Al contempo, è presente un tentativo di numerizzazione di Enti comunque astratti. A un livello per così dire, fondamentale, si presentano i casi già noti dell'Analisi, vale a dire lo spazio euclideo Rⁿ e relativi oggetti ivi definiti come applicazioni, omeomorfismi, diffeomorfismi, etc. In tale livello l'identificazione dei punti con i numeri è immediata. Basti pensare all'introduzione dei riferimenti cartesiani, i quali ci permettono di "etichettare" i singoli punti con i numeri reali. In tal modo una qualunque retta si identifica con lo spazio euclideo R¹. Basta infatti assegnare un riferimento cartesiano R(Ox), per cui la variabile reale

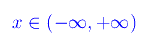
ci permette di etichettare ogni punto con un numero reale. In questa lezione abbiamo visto come dotare Rⁿ di una struttura topologica. Più specificatamente, nello spazio R¹ con la topologia euclidea gli aperti sono (oltre a R¹ e al vuoto Ø) gli intervalli del tipo (a,b) con a,b reali e a0 è:

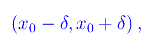
dove δ>0 può essere preso arbitrariamente piccolo. Tutto ciò esibisce una estensione immediata a Rⁿ, per ogni intero naturale n=1. Quando invece passiamo a considerare insiemi qualsiasi i cui elementi non sono punti nel senso geometrico del termine, l'unico modo per "geometrizzarli" consiste nel cercare di stabilire una qualche corrispondenza biunivoca con Rⁿ. Infatti, nella definizione di varietà topologica abbiamo richiesto l'esistenza di una legge che ad aperti di un assegnato spazio di Hausdorff faccia corrispondere aperti di Rⁿ e viceversa. In tale definizione si apre il problema della determinazione dell'intero naturale n, ovvero della dimensione della varietà topologica che stiamo esaminando. Diciamo per ora che si tratta di un problema che richiede una condizione più forte di quella di spazio di Hausdorff. E ci aspettiamo che l'intero n dipenda dal "punto" considerato; tale circostanza restituisce uno spazio a dimensione variabile, ovvero un ente completamente anti-intuitivo.

Consideriamo ora un insieme non vuoto che non ha nulla a che vedere con R. Precisamente, immaginiamo di avere due palline una nera, l'altra bianca. Denotiamo quindi con S l'insieme i cui elementi sono le predette palline:

L'insieme delle parti di S è:

che come è noto, definisce la topologia discreta. Abbiamo cioè lo spazio topologico:

I "punti" di tale spazio sono gli elementi di S, ovvero la pallina nera e quella bianca. Gli aperti sono tutti e soli gli elementi dell'insieme delle parti, mentre gli intorni di singolo punto sono:

Lo spazio topologico che abbiamo costruito è uno spazio di Hausdorff. Infatti, ogni coppia di punti distinti ammette una coppia di intorni disgiunti. Qui l'unica coppia distinta è (nera,bianca), quindi gli intorni {nera},{bianca} tali che

Si noti che abbiamo implementato una gerarchia del tipo

Man mano che si scende in tale gerarchia troviamo una "condizione più forte": uno spazio topologico è "qualcosa di più" di un insieme di elementi. Allo stesso modo, uno spazio di Hausdorff è un caso speciale di spazio topologico. Nell'ultima freccia c'è un punto interrogativo, perchè nel caso dell'insieme composto da due uniche palline che per quanto visto è "hausdorffiabile", ancora non sappiamo se può essere dotato di una struttura di varietà topologica, che è qualcosa di ancora "più forte". Proviamoci. La definizione di varietà topologica ci impone: Comunque prendiamo un elemento di {nera,bianca} esiste un intorno di tale elemento omemorfo a un aperto di Rⁿ. Scriviamo

Iniziamo con la pallina nera. Abbiamo visto che un suo intorno è l'insieme {nera}. Proviamo allora a "forzare" questo intorno, nel senso che cercheremo di metterlo in corrispondenza biunivoca e bi-continua con un qualche aperto di Rⁿ. Il problema è: quale n? Proviamo con n=1:

Cioè alla pallina nera facciamo corrispondere il numero reale 0.

Vediamo se tale applicazione è continua nella topologia dei singoli spazi. Applichando la definizione, deve risultare:

Ora non dobbiamo fare altro che specificare i singoli intorni. Si ha:s

mentre V_nera può essere uno dei due aperti

Prendiamo

per cui

cioè φ_nera è continua. Allo stesso modo si dimostra la continuità di φ_nera, ed è facile vedere che entrambe sono iniettive, suriettive con inversa continua. Cioè sono omeomorfismi, e possiamo quindi asserire che il nostro insieme di una pallina bianca e di una pallina nera, strutturato come spazio topologico con topologia discreta, è una varietà topologica. Di quale dimensione? A occhio sembra arbitraria, perché il ragionamento seguito per stabilire l'esistenza degli omemorfismi sembra funzionare per ogni n. In altri termini, avremmo potuto scrivere

---

---

Tags: punti, spazio di hausdorff, spazio euclideo, topologia, varietà topologica

Articoli correlati