[¯|¯] Definizione assiomatica di curva

Marzo 26th, 2017 | by Marcello Colozzo |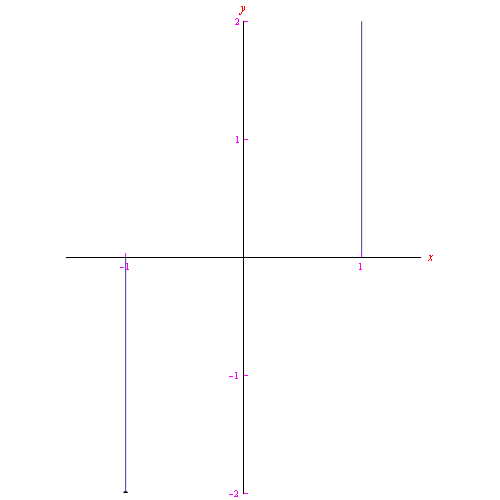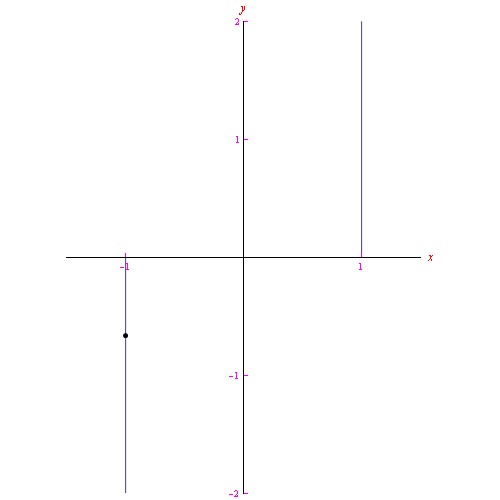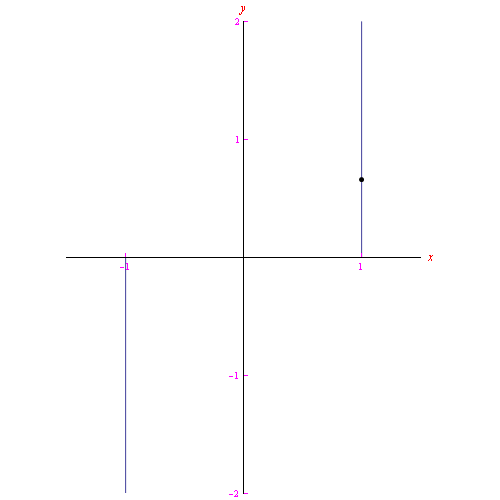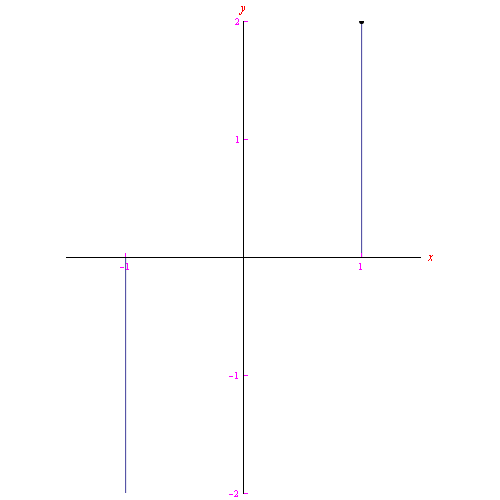

curva,rappresentazione parametrica,intervallo base,parametro — **Fig. 1.**

La nozione di curva nello spazio euclideo R³ è un concetto primitivo assiomatizzabile. Invero, sussiste la seguente definizione:
Definizione
Per un'assegnata curva Γ di R³, esiste una funzione vettoriale di classe C° su un intervallo X di R

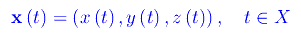
tale che

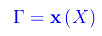
cioè Γ è l'immagine di X mediante x(t) o ciò che è lo stesso, è il codominio della funzione x(t).
La funzione vettoriale x(t) che definisce le coordinate cartesiane dei punti di Γ, si chiama rappresentazione parametrica di Γ, mentre l'intervallo di definizione X è la base della rappresentazione e la variabile reale t definisce il parametro della rappresentazione.

L'appartenenza a C° assicura che Γ sia una curva continua, ovvero priva di interruzioni. Ad esempio, consideriamo in R² il luogo geometrico Γ quale codominio della funzione vettoriale:

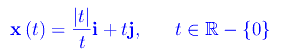
Tale funzione vettoriale non è continua in t=0, giacché

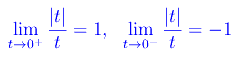
Più precisamente, il luogo Γ è l'unione delle semirette

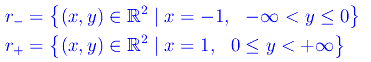
Il luogo geometrico Γ presenta una evidente interruzione in corrispondenza del valore t=0, come vediamo dal grafico:

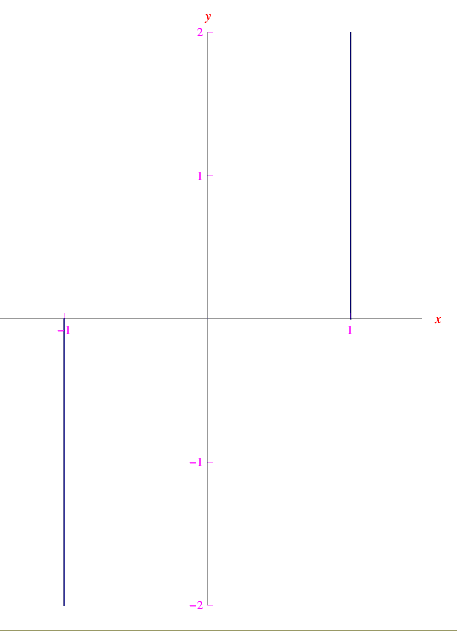
Utilizzando un linguaggio impreciso ma efficace, diremo che Γ è una "retta spezzata". Immaginando un punto mobile che percorre Γ, se il parametro t segna il tempo, si ha che all'istante t=0 il punto passa istantaneamente dalla posizione (-1,0) alla posizione (0,1), come illustrato nella figura animata 1 (al top di questa pagina).

Vai alla lezione successiva

Vai alla lezione precedente

Indice delle lezioni

No TweetBacks yet. (Be the first to Tweet this post)