[¯|¯] Forze non lipschitziane: per ora non c’è molto da dire |

[¯|¯] Forze non lipschitziane: per ora non c'è molto da dire

Marzo 8th, 2017 | by Marcello Colozzo |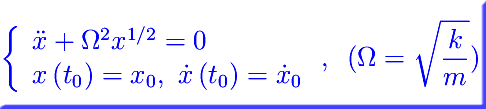

equazioni differenziali,problema di Cauchy,condizione di Lipschitz

Forze non lipschitziane

Riprendiamo il caso dell'oscillatore armonico. Qui è

per cui il corrispondente problema di Cauchy è:
equazioni differenziali,problema di Cauchy,condizione di Lipschitz

La funzione f(x) è manifestamente lipschitziana, per cui il predetto problema è compatibile e determinato i.e. ammette una ed una sola soluzione. Ne consegue, come è ben noto, che l'evoluzione di tale sistema è deterministica.

Consideriamo ora il seguente campo di forze

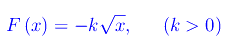
La forza per unità di massa è

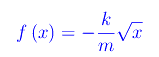
Tale funzione non è lipschitziana in quanto la derivata prima diverge in x=0:
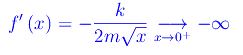
equazioni differenziali,problema di Cauchy,condizione di Lipschitz

È facile convincersi che al pari delle forze elastiche, anche questo campo è attrattivo. Il corrispondente problema di Cauchy si scrive:

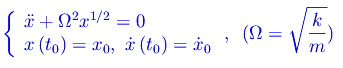
Per quanto precede, la condizione di Lipschitz è una condizione sufficiente ma non necessaria, per cui ciò non implica la non unicità delle soluzioni del corrispondente problema di Cauchy, nel senso che le soluzioni vanno esaminate caso per caso. In ogni modo, nella situazione in esame l'equazione differenziale è non lineare, e per la sua integrazione ci affidiamo a Mathematica. Tuttavia le soluzioni di questo caso specifico non dicono granché su una eventuale indeterminazione sulle soluzioni e quindi sull'evoluzione dinamica dello stato meccanico, per cui per ora lo lasciamo in sospeso.

No TweetBacks yet. (Be the first to Tweet this post)