[¯|¯] Infinitesimo di ordine non inferiore [superiore] rispetto ad un altro infinitesimo

Febbraio 22nd, 2017 | by Marcello Colozzo |

infinitesimi,infiniti,infinitesimi confrontabili,ordine,infinitesimi non confrontabili

Fig. 2

Esempio 1
Siano dati gli infinitesimi (per x->0):

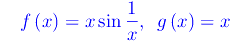
infinitesimi,infiniti,infinitesimi confrontabili,ordine,infinitesimi non confrontabili

Il rapporto è non regolare
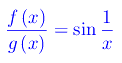
infinitesimi,infiniti,infinitesimi confrontabili,ordine,infinitesimi non confrontabili

Passando ai valori assoluti di singolo infinitesimo, constatiamo che nemmeno ora il rapporto è regolare, giacché:

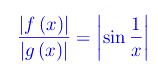
infinitesimi,infiniti,infinitesimi confrontabili,ordine,infinitesimi non confrontabili

Tuttavia

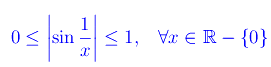
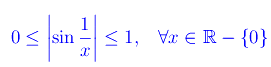
infinitesimi,infiniti,infinitesimi confrontabili,ordine,infinitesimi non confrontabili

infinitesimi,infiniti,infinitesimi confrontabili,ordine,infinitesimi non confrontabili

Ne consegue che f(x)=xsin(1/x) è (in x=0) un infinitesimo di ordine non inferiore a g(x)=x. In fig. 1 riportiamo i grafici di tali funzioni in un intorno di x=0.

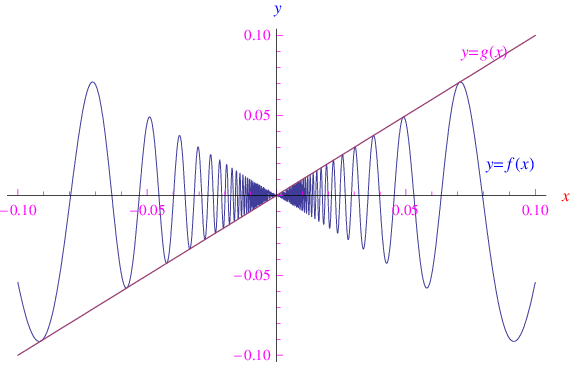
infinitesimi,infiniti,infinitesimi confrontabili,ordine,infinitesimi non confrontabili

Fig. 1. Grafico delle funzioni f(x)=xsin(1/x) e g(x)=xsin²(1/x) entrambe infinitesime per x->0. Il rapporto |f(x)|/|g(x)| è limitato inferiormente ma non superiormente, per cui f(x) è di ordine non superiore a g(x).


Esempio 2
Siano

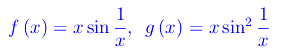
infinitesimi,infiniti,infinitesimi confrontabili,ordine,infinitesimi non confrontabili

Si tratta di infinitesimi in x=0. Il primo limite è ben noto:
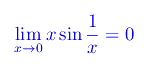
infinitesimi,infiniti,infinitesimi confrontabili,ordine,infinitesimi non confrontabili

Il secondo è meno immediato, ma facilmente dimostrabile applicando il teorema dei carabinieri:
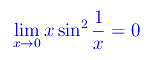
infinitesimi,infiniti,infinitesimi confrontabili,ordine,infinitesimi non confrontabili









Confrontiamo i due infinitesimi eseguendo il rapporto:

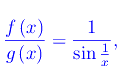
infinitesimi,infiniti,infinitesimi confrontabili,ordine,infinitesimi non confrontabili

Ma

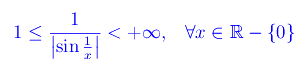
infinitesimi,infiniti,infinitesimi confrontabili,ordine,infinitesimi non confrontabili

Ne consegue che f(x)=xsin(1/x) è (in x=0) un infinitesimo di ordine non superiore a g(x)=xsin²(1/x). In fig. 1riportiamo i grafici di tali funzioni in un intorno di x=0.








No TweetBacks yet. (Be the first to Tweet this post)

Tags: , , , ,

Articoli correlati

Commenta l'esercizio