[¯|¯] Studio di curve piane in coordinate polari. La spirale logaritmica
Dicembre 8th, 2016 | by Marcello Colozzo |
Con questo post inauguriamo la stesura di un handbook dedicato allo studio di curve piane in coordinate polari. Rammentiamo che l'equazione che rappresenta una curva in un assegnato sistema di coordinate, può assumere forme differenti. Ad esempio, si può considerare il grafico di una funzione f(x):
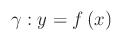
Diversamente, la curva può essere data in forma parametrica:

o in forma implicita:

In quest'ultimo caso si cerca di "forzare" la variabile y esprimendola in funzione di x, utilizzando il teorema del Dini. Di particolare interesse sono le curve in coordinate polari. Precisamente, assegnato un riferimento polare con polo nell'origine del corrispondente riferimento cartesiano R(Oxy) e asse polare coincidente con l'asse x, l'equazione che rappresenta una curva piana in coordinate polari è r=r(φ) dove (r,φ) sono rispettivamente il raggio vettore e l'anomalia, ovvero le coordinate polari. Rammentiamo le equazioni che legano queste ultime alle coordinate cartesiane:

Spirale logartimica
La spirale logaritmica ha equazione:
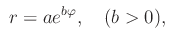
In questa sezione dimostreremo una importante proprietà della spirale logaritmica, espressa dal seguente teorema:
Teorema
Sia P un punto variabile sulla spirale logaritmica. La retta tangente alla curva in P, interseca il raggio vettore secondo un angolo costante.
Dimostrazione
Consultare gli appunti in formato pdf



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











