[¯|¯] Base e dimensionalità dello spazio vettoriale i cui elementi sono tensori covarianti di rango r

Marzo 2nd, 2020 | by Marcello Colozzo |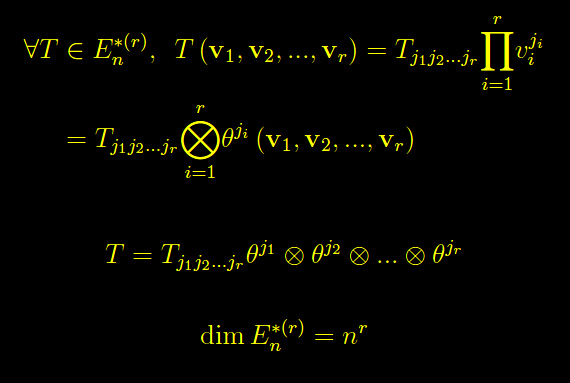

tensori covarianti,rango,spazio vettoriale,prodotto tensoriale

Ciò premesso per un assegnato

denotiamo con {θ^j_i} la base duale associata alla base {e_{k_i}} di E_n. Quindi

ed è chiaro che

Possiamo allora considerare un particolare sistema di elementi dello spazio vettoriale

Precisamente:

Ad esempio, per un tensore covariante di rango 2 quale elemento di

su ha

ossia 9 elementi. In generale:

Dimostriamo il seguente teorema:
Teorema
Il sistema

è una base di E_n^*(r)

Dim.

Dimostriamo innanzitutto che si stratta di un sistema linearmente indipendente di ordine massimo. Comunque prendiamo una r-pla di vettori di E_n, dovrà essere per definizione di prodotto tensoriale di r 1-forme:

cioè

Scriviamo (con ovvio significato dei simboli):

Tenendo conto dell'equazione scritta più sopra:

Se in particolare, prendiamo i vettori di base:

onde la precedente diviene:

Ne consegue che il sistema

è lineramente indipendente. È facile convincersi che si tratta di un sistema di ordine massimo e ogni tensore covariante di rango r si esprime in un sol modo come combinazione lineare degli elementi del predetto sistema. Infatti:

Cioè

E quindi

c.d.d.