[¯|¯] Spunta nuovamente il paradosso di Russell
Giugno 14th, 2018 | by Marcello Colozzo |
Definizione
Dicesi insieme di indici un insieme non vuoto K (finito o infinito). Una famiglia di insiemi dipendente dall'insieme di indici K, è univocamente determinata da una legge che associa ad ogni k di K, un insieme Ak. Tale ente è simboleggiato da
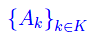
Ciò premesso, sussiste la seguente definizione:
Definizione
Chiamasi unione degli insiemi della famiglia {Ak}, l'insieme:
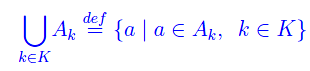
o ciò che è lo stesso
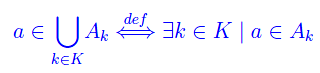
Proposizione
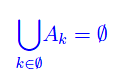
Dimostrazione
onde l'asserto.
Da tale proposizione segue
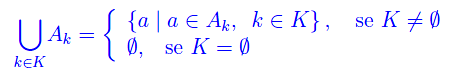
In altri termini, la definizione di unione non perde di significato se l'insieme degli indici è vuoto.
Definizione
Assegnato un insieme di indici K, dicesi intersezione degli insiemi della famiglia {Ak}, l'insieme tale che
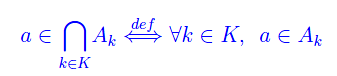
Cioè l'insieme degli elementi appartenenti a ogni insieme della famiglia.
A differenza dell'operazione di unione, l'operazione di intersezione perde di significato se l'insieme degli indici è vuoto, giacché la condizione
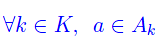
svanisce, nel senso che è verificata da ogni elemento a. Ciò implica che

Ma in virtù del paradosso di Russel, tale ente non è un insieme.
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.
No TweetBacks yet. (Be the first to Tweet this post)
Tags: famiglia di insiemi, intersezione, paradosso di russel, unione
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











