[¯|¯] Applicazioni suriettive, iniettive, bi-iettive
Giugno 8th, 2018 | by Marcello Colozzo |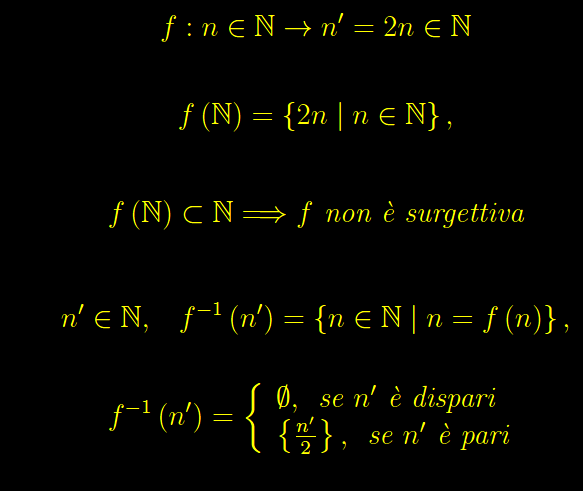
Definizione
Un'applicazione f:S->S' si dice suriettiva (o surgettiva o che è una surgezione) se f(S)=S', cioè se ogni elemento x' di S' proviene, attraverso f, da un elemento x di S.
Questi esempi mostrano applicazioni surgettive.
Definizione
Un'applicazione f:S->S' si dice iniettiva se

cioè se la controimmagine di ogni elemento di f(S) è costituita da un solo elemento. Ne consegue che se f è iniettiva, ogni elemento di x di f(S) proviene da un solo elemento x di S. Posto
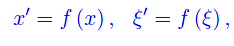
si ha

Esempio
Denotiamo con N l'insieme degli interi naturali. Sia data l'applicazione che a ogni intero n associa il doppio 2n:
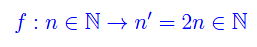
Segue
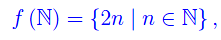
cioè l'immagine di N mediante f è l'insieme dei numeri pari:
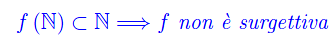
Determiniamo la controimmagine:
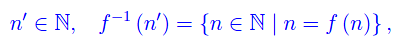
onde
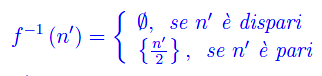
Ne concludiamo che f è iniettiva.
Definizione
Un'applicazione f:S->S' si dice bi-iettiva o che è una bi-iezione se è suriettiva e iniettiva.
Applicazione identica e applicazione costante
Definizione
Comunque prendiamo un insieme S non vuoto, dicesi applicazione identica, l'applicazione:
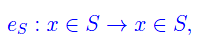
cioè l'applicazione che associa a ogni elemento x di S, l'elemento medesimo.
Riesce

da cui la bi-iettività di eS.
Definizione
Un'applicazione f:S->S' si dice costante se

cioè se ogni elemento x di S muta mediante f, in un elemento fisso di f(S).
Sostienici
No TweetBacks yet. (Be the first to Tweet this post)
Tags: applicazioni bi-iettive, Applicazioni iniettive, Applicazioni suriettive, Applicazioni tra insiemi
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











