» Esercizi svolti di Matematica e Fisica

[¯|¯] La definizione di spazio metrico

Si definisce spazio metrico un insieme X sul quale è definita una funzione

La metrica più nota è quella definita su uno spazio vettoriale normato, ossia uno spazio vettoriale dotato di norma ||.||, mediante la formula:

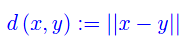
Se lo spazio vettoriale è Rⁿ e || || è la norma euclidea, la precedente formula diventa:

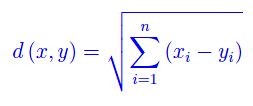
e ci fornisce la distanza euclidea tra due punti x e y di Rⁿ ovvero la lunghezza del segmento che li unisce. Questa è indubbiamente la distanza più comune, quella nota a tutti, anche ai non matematici. Ma in matematica esistono infinite metriche, alcune delle quali apparentemente “strambe”. Vediamone qualcuna.
Consideriamo un insieme arbitrario X e poniamo:

con x,y appartenenti a X. Tale funzione prende il nome di metrica discreta e, anche se può sembrare assurdo (ogni elemento di X dista 1 da tutti gli altri), è effettivamente una distanza. Per dimostrarlo basta dimostrare che d(x, y) soddisfa tutte e quattro le proprietà che definiscono una metrica. Le prime tre si verificano immediatamente; per provare che vale anche la disuguaglianza triangolare, basta considerare i casi possibili:

Posted in topologia | No Comments »

[¯|¯] Spazi topologici con metrica data da un processo aleatorio

Fenomeni del tipo NDE e addirittura l'Entanglement Quantistico potrebbero essere spiegati congetturando una natura aleatoria della metrica dello spazio in cui si verificano i suddetti processi. In tal modo, oggetti che sono spazialmente separati, in realtà hanno una distanza infinitesima (e in ciò rientrerebbero anche i fenomeni di visione remota).
(altro…)

Posted in Fisica Teorica | No Comments »