Tre teoremi sulla convergenza non assoluta di una serie numerica
giovedì, Ottobre 21st, 2021
Nei numeri precedenti abbiamo stabilito che la convergenza assoluta è una condizione sufficiente per la convergenza di una serie. Tuttavia, tale condizione non è necessaria. Enunciamo (senza dimostrare) tre teoremi sulla convergenza non assoluta.
Teorema 1
Hp
La successione delle somme parziali {Sp} relative a una assegnata serie
è superiormente limitata. Inoltre, la successione di numeri reali non negativi {cn} è non crescente ed infinitesima.
Th
La serie
è convergente.
Teorema 2
Hp
La serie
è convergente. Inoltre, la successione di numeri reali {cn} è non crescente ed inferiormente limitata.
Th
La serie
è convergente.
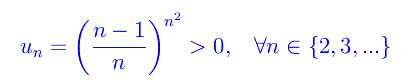
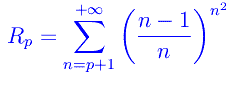
Congettura di Riemann
Trasformata discreta di Fourier
Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier 
Infinitesimi ed infiniti
Limiti notevoli
Punti di discontinuità
Misura di Peano Jordan
Eserciziario sugli integrali
Differenziabilità 
Differenziabilità (2)
Esercizi sui limiti
Appunti sulle derivate
Studio della funzione
Esercizi sugli integrali indefiniti
Algebra lineare
Analisi Matematica 2
Analisi funzionale
Entanglement quantistico
Spazio complesso
Biliardo di Novikov
Intro alla Meccanica quantistica
Entanglement Quantistico
