Una curva regolare può avere una rappresentazione parametrica non regolare?

giovedì, Dicembre 17th, 2020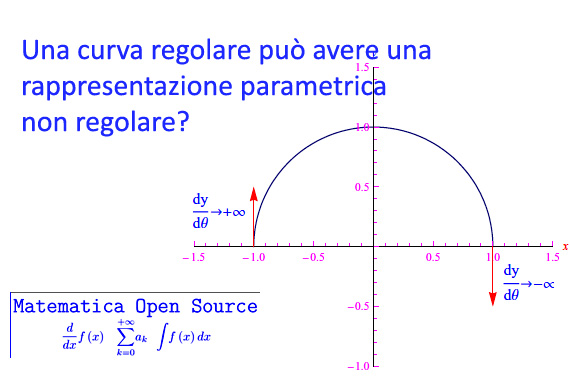

curva regolare,rappresentazione parametrica regolare,rappresentazione parametrica non regolare — **Fig. 1**

La risposta è sì. Ad esempio, consideriamo in R² la semicirconferenza di raggio unitario centrata nell'origine e tracciata nel semipiano xy. Una rappresentazione parametrica regolare è

Tuttavia, il medesimo luogo geometrico esibisce quest'altra rappresentazione parametrica:

che è non regolare. Infatti, la derivata prima ha una discontinuità di seconda specie agli estremi dell'intervallo base.

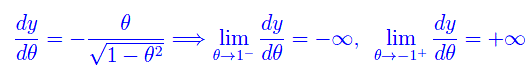
come illustrato in fig. 1.

Ne concludiamo che esistono infinite rappresentazioni parametriche non regolari di un'assegnata curva regolare. In altri termini, la non regolarità di una rappresentazione parametrica è condizione necessaria ma non sufficiente per la non regolarità di una curva.
(altro…)

Posted in Geometria differenziale | No Comments »

[¯|¯] Applicazione del teorema di Rolle per dimostrare l'iniettività locale di una funzione vettoriale di classe C^1 e con derivata priva di zeri

mercoledì, Febbraio 19th, 2020

rappresentazione parametrica regolare, funzione vettoriale,derivata,iniettività locale

L'esempio riportato in un numero precedente in realtà si riferisce a una rappresentazione non regolare. Infatti, una definizione rigorosa di regolarità richiede che le derivate delle funzioni componenti di una funzione vettoriale assegnata, non siano simultaneamente nulle (ovvero non devono annullarsi per lo stesso valore del parametro).
(altro…)