[¯|¯] Pallina che si muove lungo una catenaria

domenica, Marzo 1st, 2020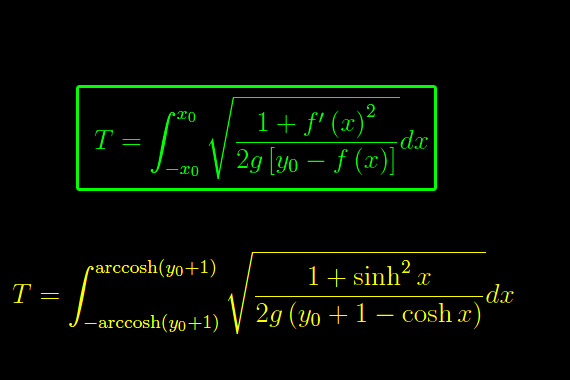

catenaria,pallina,attrito,resistenza dell'aria

Esercizio
Una pallina di massa m è lasciata cadere lungo una guida disposta in un piano verticale, avente la forma di una curva regolare concava e di equazione y=f(x), dove f(x) è una funzione pari non negativa avente un minimo relativo in x=0. 1) Studiare il moto della pallina, trascurando l'attrito e la resistenza dell'aria. 2) Considerare il caso particolare y=coshx-1.

Soluzione
Dall'esercizio precedente segue che il quadrato del modulo della velocità vettoriale della pallina è

dove y₀ è l'ordinata del punto in cui viene lasciata cadere la pallina. In particolare, consideriamo come posizione iniziale il punto A(-x₀,y₀) con x₀ > 0. Segue

per cui

(altro…)

Posted in Fisica generale 1, Meccanica analitica, meccanica razionale | No Comments »

[¯|¯] Diagramma orario e traiettoria

martedì, Febbraio 5th, 2019

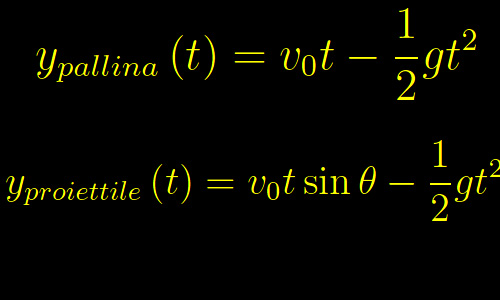
diagramma orario,traiettoria,pallina,proiettile

Esercizio
1) Il diagramma orario di una pallina lanciata verticalmente verso l'alto è una parabola concava.
2) La traiettoria di un proiettile sparato con alzo θ, è una parabola concava.
Esiste un legame funzionale tra 1 e 2? (Si trascuri la resistenza dell'aria)

Soluzione
Caso 1
Orientando un asse y verticale verso l'alto, l'equazione oraria della pallina è:

ove v₀ è il modulo della velocità iniziale. Il diagramma orario i.e. il grafico della funzione (scritta più sopra) è una parabola concava passante per l'origine.
(altro…)