[¯|¯] L'insieme di Cantor e la rappresentazione in base 3
venerdì, Aprile 7th, 2017
Fig. 1
Dal momento che nella costruzione dell'insieme di Cantor entrano in gioco intervalli di ampiezza 1/3k, si ha che tale insieme deve essere in qualche modo collegato alla rappresentazione dei reali x appartenenti all'aperto (0,1) in base 3. Infatti l'espansione in base 3 di x del predetto intervallo si scrive:
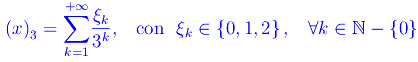
essendo in generale
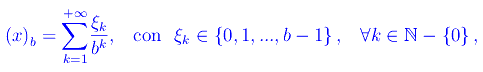
dove b>1 è la base della rappresentazione. Se b=10 si ha per così dire l'espansione usuale, cioè in base 10
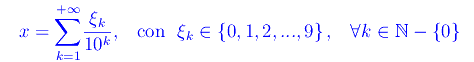
Esempio
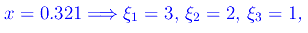
onde

Esempio

Scriviamo la rappresentazione in base 3 del numero periodico 0.020202...
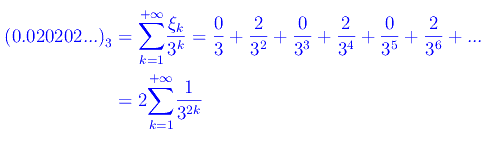
Ma

per cui

In che modo l'insieme di Cantor è collegato all'espansione in base 3? Per rispondere a questa domanda guardiamo il procedimento ricorsivo che restituisce il k-esimo insieme Ck:
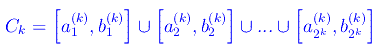
Per k=1
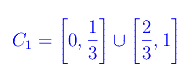
Se osserviamo gli estremi dell'intervallo rimosso, cioè i punti 1/3 e 2/3, ci rendiamo conto che
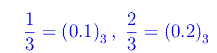
Cioè nella rappresentazione in base 3, al primo step (k=1) rimuoviamo l'intervallo aperto di estremi (0.1)3,(0.2)3. Il secondo step ricorsivo (k=2) restituisce l'insieme

Qui vediamo che sono stati rimossi gli intervalli aperti
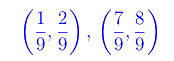
Ma
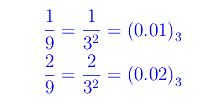
(altro…)







 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











