[¯|¯] Infinitesimi ed infiniti di ordine indeterminato
sabato, Febbraio 25th, 2017
Fig. 1. Per x->0+ la funzione x*ln(x) è un infinitesimo di ordine inferiore a 1, ma maggiore di un qualunque 0<α<1. Per x->+oo è un infinito di ordine superiore a 1, ma minore di un qualunque α>1.
Rammentiamo che con il simbolo I(x0) denotiamo la classe degli infinitesimi in x0 e non definitivamente nulli intorno a tale punto. Ciò premesso, sussiste la seguente definizione
Definizione
Se u(x) è l'infinitesimo di riferimento nella predetta classe, diremo che l'infinitesimo f non ha un ordine determinato, se il rapporto f(x)/[u(x)]α è regolare per ogni α>0, riuscendo convergente per alcuni valori di α, divergente per i rimanenti.
Esempio
Consideriamo la funzione:
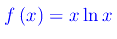
Risulta
onde f(x) è un infinitesimo in x=0. Dal momento che x->0+, assumiamo come infinitesimo di riferimento la funzione:
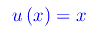
Quindi
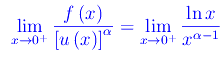
Distinguiamo i casi:
-
0<α<1
onde f(x) è un infinitesimo di ordine superiore ad α per ogni 0<α<1. - α>=1
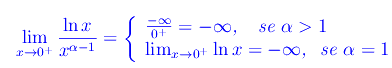
Cioè f(x) è un infinito di ordine inferiore a 1.
Ne consegue che x*ln(x) è un infinitesimo (in x=0) di ordine inferiore a 1, ma maggiore di un qualunque 0<α<1. (altro…)
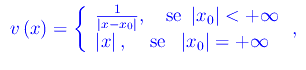
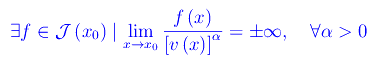
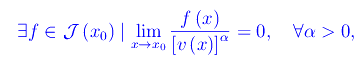
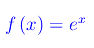
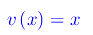
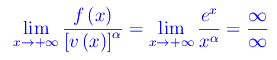
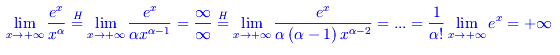
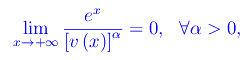
Congettura di Riemann
Trasformata discreta di Fourier
Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier 
Infinitesimi ed infiniti
Limiti notevoli
Punti di discontinuità
Misura di Peano Jordan
Eserciziario sugli integrali
Differenziabilità 
Differenziabilità (2)
Esercizi sui limiti
Appunti sulle derivate
Studio della funzione
Esercizi sugli integrali indefiniti
Algebra lineare
Analisi Matematica 2
Analisi funzionale
Entanglement quantistico
Spazio complesso
Biliardo di Novikov
Intro alla Meccanica quantistica
Entanglement Quantistico
