[¯|¯] La nozione di funzione vettoriale di una variabile reale

domenica, Marzo 26th, 2017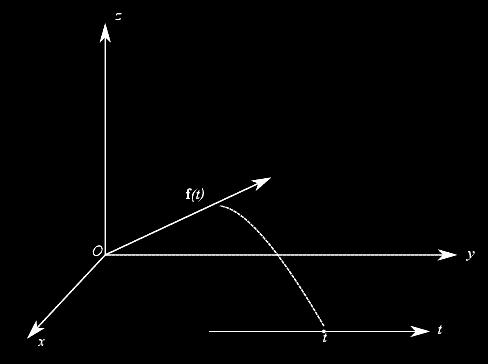

funzione vettoriale di una variabile reale,funzione scalare,limite,derivata,integrale

Fig. 1. La funzione vettoriale f associa a ogni t appartentente a X (sottoinsieme di R) il vettore f(t)=fx(t)i+fy(t)j+fz(t)k."

Definizione
Assegnato in R³ un riferimento cartesiano ortogonale K(Oxyz), una funzione vettoriale è una terna ordinata di funzioni reali di una variabile reale

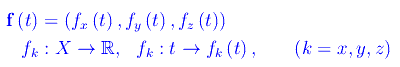
funzione vettoriale di una variabile reale,funzione scalare,limite,derivata,integrale

Quindi ad ogni t appartentente a X, f associa univocamente il vettore di componenti cartesiane fx(t),fy(t),fz(t) (cfr. fig. 1) in un assegnato riferimento cartesiano ortogonale K(Oxyz). Indicando con i,j,k i versori degli assi coordinati, si ha:

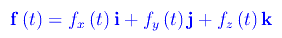
funzione vettoriale di una variabile reale,funzione scalare,limite,derivata,integrale


Denotando con · il prodotto scalare canonico nello spazio vettoriale euclideo R³, si ha la seguente definizione:
Definizione
Assegnata la funzione vettoriale:
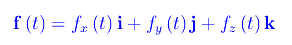
funzione vettoriale di una variabile reale,funzione scalare,limite,derivata,integrale

dicesi modulo di f, il numero reale non negativo:
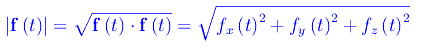
funzione vettoriale di una variabile reale,funzione scalare,limite,derivata,integrale


(altro…)



Posted in Geometria differenziale, Meccanica analitica, meccanica razionale | No Comments »