La normale a una curva è la tangente alla sua evoluta

lunedì, Dicembre 28th, 2020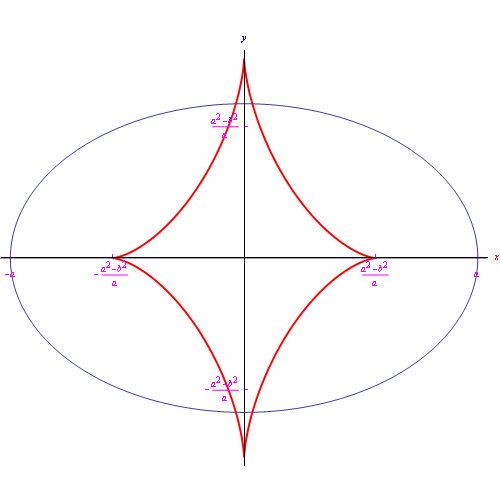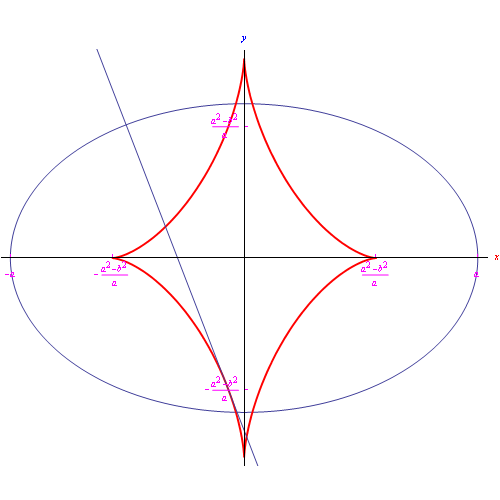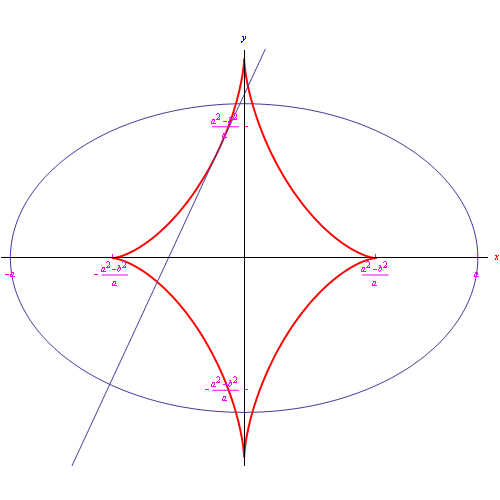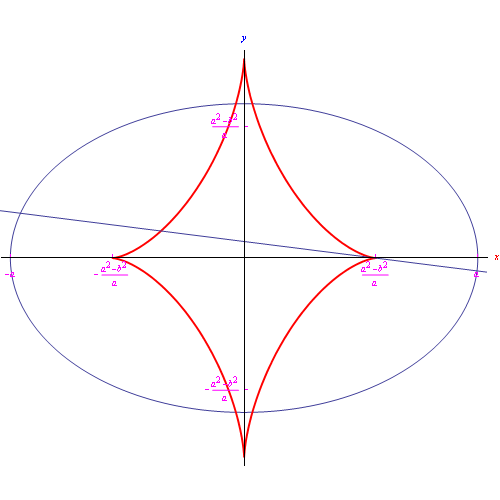

evoluta,normale,tangente,curva — **Fig. 1**

In base al teorema 4, la retta tangente all'evoluta &gamma:* in un generico punto C, è la normale all'evolvente γ nel punto P tale che C è centro di curvatura in quel punto. In altri termini, la normale a una curva è la tangente alla sua evoluta. Ne consegue che l'evoluta di una curva ? è l'inviluppo delle normali a γ. Questa notevole proprietà dell'evoluta si traduce in un efficace algoritmo per la determinazione di tale luogo geometrico. Ad esempio, nel caso dell'esercizio precedente proviamo a scrivere l'equazione della famiglia delle normali all'ellisse:

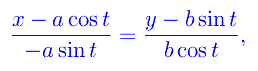
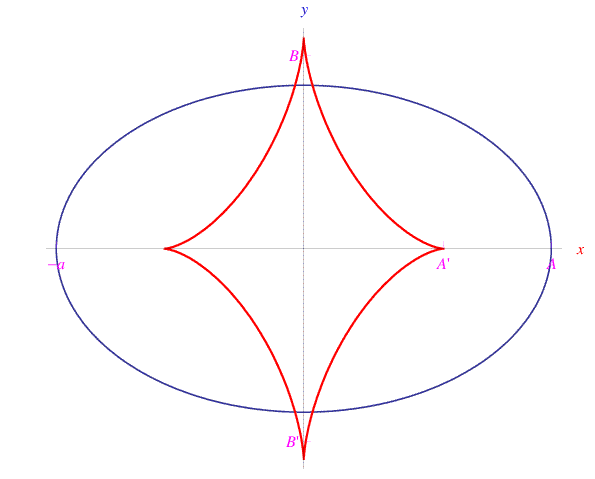
Nel frattempo guardando la fig.

constatiamo quanto appena asserito e cioè: la normale all'ellisse è la tangente alla sua evoluta.

Per determinare l'equazione della normale all'ellisse procediamo nel seguente modo: scriviamo l'equazione della tangente in un generico punto, ossia

dopodiché scriviamo l'equazione della retta perpendicolare alla tangente. A tale scopo osserviamo che una coppia di numeri direttori della tangente è

Dalla geometria analitica sappiamo che una coppia di numeri direttori (?',µ') della retta perpendicolare deve essere tale che

Ad esempio

è una tale coppia. E anche

per cui l'equazione della normale è

Abbiamo dunque l'equazione della famiglia di normali a γ:

avendo definito:

A questo punto, componiamo il sistema

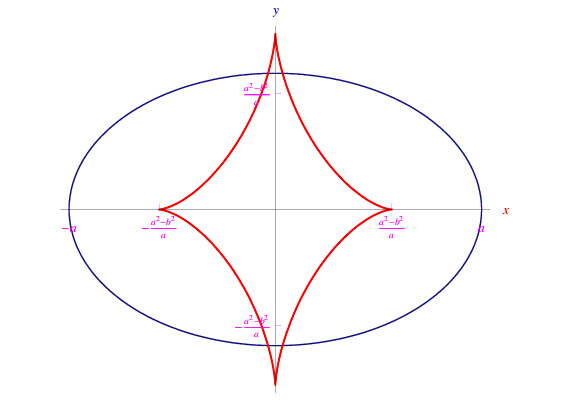
le cui soluzioni restituiscono l'equazione dell'evoluta trovata nell'esercizio precedente. Prima di concludere, applichiamo il teorema 5 per determinare la lunghezza dell'evoluta (senza calcolare un fastidioso integrale!). A tale scopo, facciamo riferimento alla fig.

nonché alla rappresentazione parametrica dell'evoluta e del raggio di curvatura dell'ellisse, ricavati dall'esercizio precedente:

La retta tangente all'evoluta nel punto A' è l'asse x, che a sua volta è la normale all'ellisse nel punto A. In tale punto è t=0, per cui il raggio di curvatura dell'ellisse è:

La retta tangente all'evoluta nel punto B' è l'asse y, che a sua volta è la normale all'ellisse nel punto B. In tale punto è t=&pi/2, per cui il raggio di curvatura dell'ellisse è:

Per il predetto teorema, la lunghezza dell'arco di estremi A',B' è

Ne consegue che la lunghezza dell'intera evoluta è

(altro…)

Posted in Geometria differenziale, Geometria II | No Comments »

Evoluta dell'ellisse

lunedì, Dicembre 28th, 2020

evoluta,ellisse,centro di curvatura — **Fig. 1**

Esercizio

Assegnata l'ellisse:

Determinare: 1) le coordinate cartesiane del centro di curvatura e il raggio di curvatura in un generico punto dell'ellisse. 2) L'equazione dell'evoluta.

Soluzione
Abbiamo dimostrato in precedenza che la curvatura è