[¯|¯] Traiettoria di un punto materiale. Equazioni finite del moto
venerdì, Marzo 24th, 2017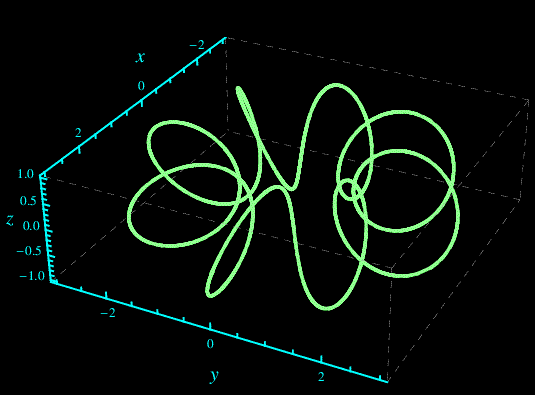
Fig. 1. Traiettoria di un punto materiale le cui equazioni finite del moto sono x=b(2+cosωt)cosωt,y=b(2+cosωt)sinωt,z=sinωt, per t variabile in [0,π] e b=1, ω=8s^-1
Nel post precedente abbiamo stabilito che per un assegnato corpo C, un osservatore Ω è in grado di costruire un insieme non vuoto

ovvero l'insieme delle posizioni di C in funzione del tempo t:
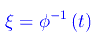
Per esplicitare tale dipendenza funzionale, è innanzitutto necessario definire lo "spazio ambiente" in cui si muove C. In Meccanica Classica si assume come ambiente del moto lo spazio euclideo 3-dimensionale E3 che noi identifichiamo semplicemente con lo spazio vettoriale euclideo R³. L'osservatore Ω verrà rappresentato da un riferimento cartesiano ortogonale K(Oxyz) che definisce un sistema di riferimento noto come terna solidale a Ω.
Per fissare le idee consideriamo il caso più semplice in cui C è un punto materiale P. Quindi:
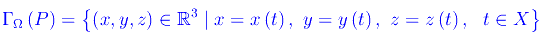
(altro…)



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











