« Previous Entries

[¯|¯] Olomorfia della derivata logaritmica della funzione zeta

mercoledì, Agosto 7th, 2019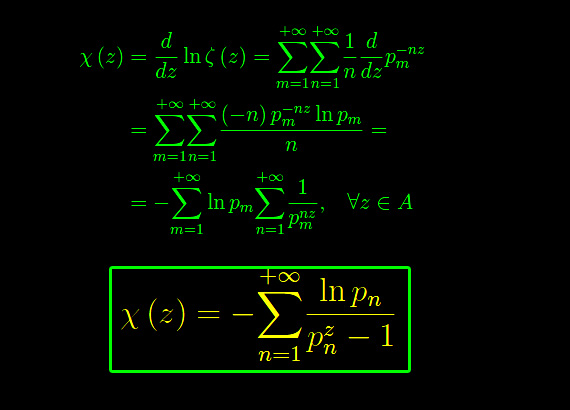

funzione zeta di riemann,olomorfia,derivata logaritmica

Nel numero precedente abbiamo dimostrato che gli zeri della funzione zeta sono le singolarità della derivata logaritmica. Scriviamo ora la formula della funzione zeta nella forma euleriana:


il cui campo di convergenza è il seguente campo a connessione lineare semplice:

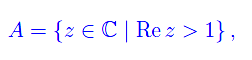
rammentando che la funzione zeta è olomorfa in A. Inoltre, è stato dimostrato che la zeta è ivi priva di zeri. Prendiamo con le dovute cautele il logaritmo della zeta:


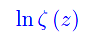
(altro…)



Posted in Teoria dei numeri | No Comments »

[¯|¯] Gli zeri della funzione zeta di Riemann sono le singolarità della sua derivata logaritmica

martedì, Agosto 6th, 2019

funzione zeta di riemann,zeri,singolarità,derivata logaritmica

Se z=x+iy è l'usuale variabile complessa, la funzione zeta di Riemann è definita come:


dove il pedice HE denota l'estensione olomorfa i.e. il prolungamento analitico della funzione assegnata. Ricordiamo che la funzione zeta è olomorfa in tutto C tranne nel punto z=1, dove ha un polo semplice:

Si tratta, quindi, di una funzione meromorfa.
(altro…)



Posted in Analisi Matematica III | No Comments »

« Previous Entries