[¯|¯] Retta tangente a una curva piana in forma implicita

giovedì, Marzo 30th, 2017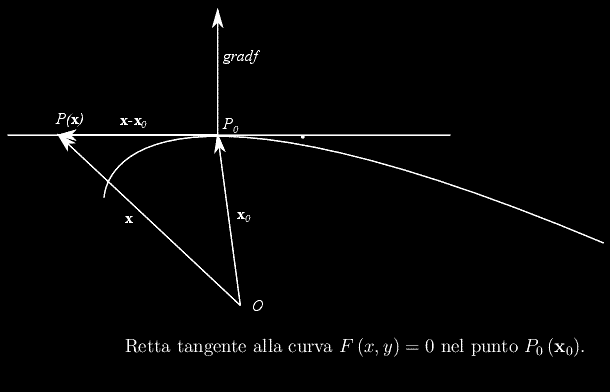

curva piana in forma implicita,teorema del dini, curva regolare,retta tangente — **Fig. 1**

Sia Γ una curva piana la cui equazione in forma implicita è

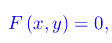
curva piana in forma implicita,teorema del dini, curva regolare

dove F è un elmento di C¹(A) con A insieme aperto di R². Per quanto visto se

in un intorno di tale punto la curva Γ è un arco regolare. Per fissare le idee supponiamo:

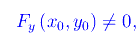
per cui

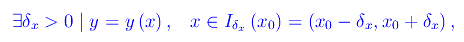
e la rappresentazione parametrica
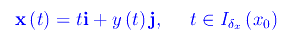
curva piana in forma implicita,teorema del dini, curva regolare

è regolare. Ne consegue che la curva Γ si compone di archi regolari. La regolarità può venir meno negli eventuali punti in cui si annulla il gradiente di F(x,y), cioè le soluzioni dell'equazione

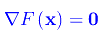
che si dicono punti singolari di Γ. Diversamente, i punti per i quali il gradiente è non nullo, sono punti non singolari di Γ.
(altro…)

Posted in Geometria differenziale, Meccanica analitica | No Comments »

[¯|¯] Curve piane in forma implicita

giovedì, Marzo 30th, 2017

Riprendiamo il Fasano - Marmi (Meccanica Analitica) a pag. 4

Nella definizione 1.2 bisognerebbe aggiungere l'appartenenza della funzione vettoriale x(t) alla classe C¹. Ciò è una conseguenza del Teorema del Dini. Infatti, procedendo in generale:
Una curva piana Γ può essere "implicitamente" rappresentata da un'equazione:
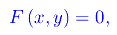
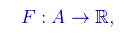
curva piana in forma implicita,teorema del dini, curva regolare

dove

essendo A un insieme aperto (campo) di R². In altri termini, la curva Γ è l'intersezione del grafico della funzione F(x,y) con il piano coordinato xy. In alcuni casi possiamo "forzare" la variabile y esprimendola in funzione di x, utilizzando il Teorema del Dini.
(altro…)