Esercizio 5. Retta tangente a una curva piana data in forma implicita
sabato, Gennaio 2nd, 2021
Esercizio
Assegnata la curva
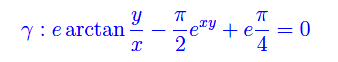
1) Scrivere l'equazione della tangente in P(2,0)
2) Classificare gli eventuali punti singolari.
Soluzione
Poniamo
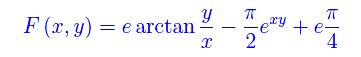
L'equazione della retta tangente è

Calcoliamo le derivate parziali:

Segue

Quindi l'equazione richiesta:

Per il quesito 2 dobbiamo risolvere il sistema:
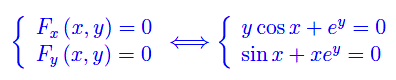
Si noti che la funzione F(x,y) non è definita sull'asse y, mentre le derivate parziali rispetto alle variabili x e y, sono ivi definite con esclusione dell'origine (0,0). Ne segue che dobbiamo escludere dalle eventuali soluzioni i punti dell'asse y. Risolvendo con Mathematica otteniamo i seguenti punti singolari:

Per classificarli dobbiamo valutare
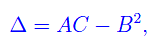
dove

A tale scopo determiniamo le derivate parziali seconde:
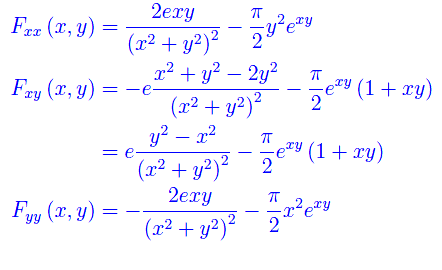
Segue
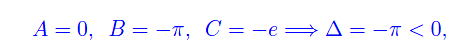
per cui i predetti punti sono nodi (punti doppi). Sfortunatamente non è possibile tracciare la curva via software. Ne possiamo avere un'idea da come il grafico z=F(x,y) interseca il piano z=0 (fig. 1).
(altro…)


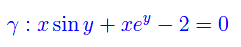
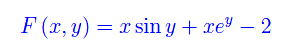

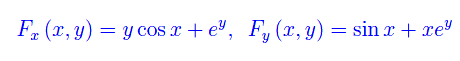




 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











